КРИВЫЕ, КАК ТРАЕКТОРИИ
ДВИЖЕНИЯ ТОЧЕК
Кривые
с древних времен привлекали к себе внимание ученых и использовались ими
для описания различных природных явлений от траектории брошенного камня
до орбит космических тел.
В школьном
курсе математики в качестве кривых рассматриваются в только графики функций.
При этом основное внимание уделяется их аналитическим свойствам, возрастанию,
убыванию и т. п. Геометрические же свойства остаются в стороне даже для
таких известных кривых как парабола, эллипс, гипербола. Знакомство с кривыми,
изучение их свойств позволит расширить геометрические представления, углубить
знания, повысить интерес к геометрии, создаст содержательную основу для
дальнейшего изучения математики, физики и др. наук.
В учебнике
геометрии для 7-9 классов [1] рассмотрены
некоторые кривые, определяемые как геометрические места точек. Среди них:
парабола, эллипс и гипербола. Более подробно эти и другие кривые можно
изучить в курсе по выбору (элективном курсе).
Рассмотрим
кинематический способ образования кривых, при котором кривая получается
как траектория движения точки.
Пусть
окружность радиуса R катится
по прямой а. С–
точка, закрепленная на окружности, в начальный момент времени находящаяся
в положении А (рис. 1). Кривая, которую описывает точка, закрепленная
на окружности, катящейся без скольжения по прямой, называется циклоидой.
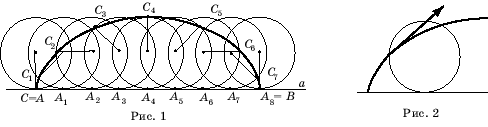 Для изображения циклоиды отложим на прямой
а
отрезок АВ, равный длине окружности, т.е. АВ = 2?R.
Разделим этот отрезок на 8 равных частей точками А1,
А2, ...,
А8
= В.
Для изображения циклоиды отложим на прямой
а
отрезок АВ, равный длине окружности, т.е. АВ = 2?R.
Разделим этот отрезок на 8 равных частей точками А1,
А2, ...,
А8
= В.
Ясно, что когда окружность,
катясь по прямой а, сделает один оборот, т.е. повернется на 360°, она займет
положение (8), а точка С переместится из положения А в положение
В.
Если
окружность сделает половину полного оборота, т.е. повернется на 180°, она
займет положение (4), а точка С переместится в самое верхнее положение
С4.
Если
окружность повернется на угол 45°, то окружность переместится в положение
(1), а точка С переместится в положение С1.
На рисунке
1 показаны также другие точки циклоиды, соответствующие оставшимся углам
поворота окружности, кратным 45°.
Соединяя
плавной кривой построенные точки, получим участок циклоиды, соответствующий
одному полному обороту окружности. При следующих оборотах будут получаться
такие же участки, т.е. циклоида будет состоять из периодически повторяющегося
участка, называемого аркой циклоиды.
Обратим
внимание на положение касательной к циклоиде (рис. 2). Если велосипедист
едет по мокрой дороге, то оторвавшиеся от колеса капли будут лететь по
касательной к циклоиде и при отсутствии щитков могут забрызгивать спину
велосипедиста.
Первым,
кто стал изучать циклоиду был Галилео Галилей (1564–1642). Он же придумал
и ее название.
Циклоида
обладает целым рядом замечательных свойств. Упомянем о некоторых из них.
Свойство
1 (Ледяная гора). В 1696 году И.Бернулли поставил задачу о нахождении
кривой наискорейшего спуска, или, иначе говоря, задачу о том, какова должна
быть форма ледяной горки, чтобы, скатываясь по ней, совершить путь из начальной
точки А в конечную точку В за кратчайшее время (рис. 3, а).
Искомую кривую назвали "брахистохроной", т.е. кривой кратчайшего времени.
Ясно,
что кратчайшим путем из точки A
в точку B является отрезок AB.
Однако при таком прямолинейном движении скорость набирается медленно и
затраченное на спуск время оказывается большим (рис. 3, б).
Скорость
набирается тем быстрее, чем круче спуск. Однако при крутом спуске удлиняется
путь по кривой и тем самым увеличивается время его прохождения.
Среди
математиков, решавших эту задачу, были: Г.Лейбниц, И.Ньютон, Г.Лопиталь
и Я.Бернулли. Они доказали, что искомой кривой является перевернутая циклоида
(рис. 3, а). Методы, развитые этими учеными при решении задачи о брахистохроне,
положили начало новому направлению математики - вариационному исчислению.
 Свойство
2 (Часы с маятником). Часы с обычным маятником не могут идти точно,
поскольку период колебаний маятника зависит от его амплитуды: чем больше
амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629–1695)
задался вопросом, по какой кривой должен двигаться шарик на нитке маятника,
чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном
маятнике кривой, по которой движется шарик, является окружность (рис. 4,а).
Свойство
2 (Часы с маятником). Часы с обычным маятником не могут идти точно,
поскольку период колебаний маятника зависит от его амплитуды: чем больше
амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629–1695)
задался вопросом, по какой кривой должен двигаться шарик на нитке маятника,
чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном
маятнике кривой, по которой движется шарик, является окружность (рис. 4,а).
Искомой
кривой оказалась перевернутая циклоида. Если, например, в форме перевернутой
циклоиды изготовить желоб и пустить по нему шарик, то период движения шарика
под действием силы тяжести не будет зависеть от начального его положения
и от амплитуды (рис. 4,б). За это свойство циклоиду называют также "таутохрона"
– кривая равных времен.
Гюйгенс
изготовил две деревянные дощечки с краями в форме циклоиды, ограничивающие
движение нити слева и справа (рис. 4,в). При этом сам шарик будет двигаться
по перевернутой циклоиде и, таким образом, период его колебаний не будет
зависеть от амплитуды.
Из этого
свойства циклоиды, в частности следует, что независимо от того, с какого
места ледяной горки в форме перевернутой циклоиды мы начнем спуск, на весь
путь до конечной точки мы затратим одно и то же время.
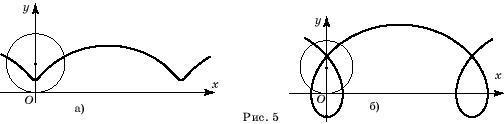
Пусть
теперь окружность катится по прямой, а точка закреплена не на окружности,
а на продолжении радуса. В этом случае точка будет описывать кривую, называемую
удлиненной циклоидой (рис. 5,а). Если же точка закреплена на радиусе внутри
окружности, то она будет описывать кривую, называемую укороченной циклоидой
(рис. 5, б).
 Рассмотрим
теперь ситуацию, при которой окружность катится без скольжения не по прямой,
а по окружности с внешней стороны. Получающаяся при этом кривая называется
эпициклоидой. В зависимости от соотношения между радиусами неподвижной
и катящейся окружностей будут получаться различные эпициклоиды. Разберем
некоторые из них.
Рассмотрим
теперь ситуацию, при которой окружность катится без скольжения не по прямой,
а по окружности с внешней стороны. Получающаяся при этом кривая называется
эпициклоидой. В зависимости от соотношения между радиусами неподвижной
и катящейся окружностей будут получаться различные эпициклоиды. Разберем
некоторые из них.
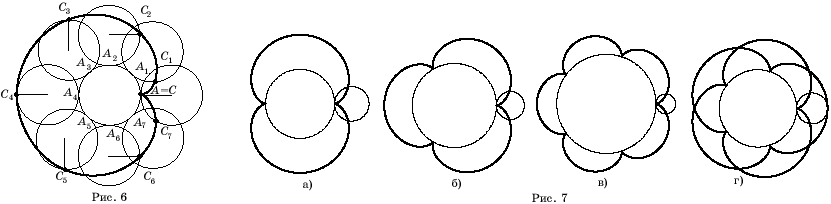
Кривая,
которая получается как траектория движения точки, закрепленной на окружности,
катящейся с внешней стороны по другой окружности того же радиуса, называется
кардиоидой.
Пусть
С
– точка, закрепленная на окружности, в начальный момент времени находится
в положении А (рис. 6). Разделим неподвижную окружность на 8 равных
частей точками А1,А2,
..., А8
= А.
Ясно,
что когда окружность сделает один оборот, т.е. повернется на 360°, она
займет исходное положение, и точка С переместится в исходное положение.
Если
окружность сделает половину полного оборота, т.е. повернется на 180°, она
займет положение (4), а точка С переместится в положение С4.
Если
окружность повернется на угол 45°, окружность переместится в положение
(1), а точка С переместится в положение С1.
На рисунке
6 показаны также другие точки кардиоиды, соответствующие оставшимся углам
поворота окружности, кратным 45°.
Соединяя
плавной кривой построенные точки, получим кривую, соответствующую одному
полному обороту окружности. При следующих оборотах окружности точка С
будет описывать ту же самую кривую.
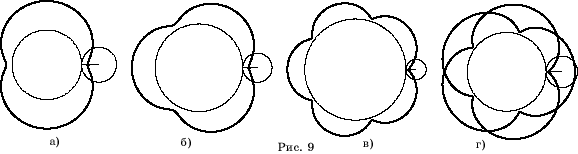
 На рисунках
7, а-г показаны траектории движения точек в случаях, когда отношение радиусов
катящейся и неподвижной окружности равно: а)
На рисунках
7, а-г показаны траектории движения точек в случаях, когда отношение радиусов
катящейся и неподвижной окружности равно: а) 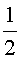 ;
б)
;
б) 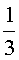 ; в)
; в) 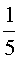 ;
г)
;
г) 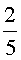 .
.
На рисунках
8 и 9 показаны соответствующие удлиненные и укороченные эпициклоиды.
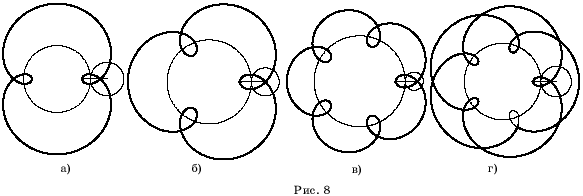
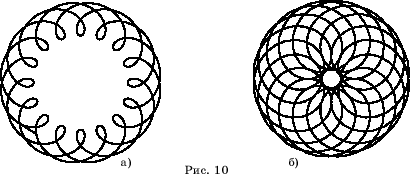
 На рисунке
10 приведены еще два примера эпициклоид, полученные с помощью компьютера
[2].
На рисунке
10 приведены еще два примера эпициклоид, полученные с помощью компьютера
[2].
 Пусть теперь
окружность катится не с внешней, а с внутренней стороны другой окружности.
Получающаяся при этом кривая называется гипоциклоидой.
Пусть теперь
окружность катится не с внешней, а с внутренней стороны другой окружности.
Получающаяся при этом кривая называется гипоциклоидой.
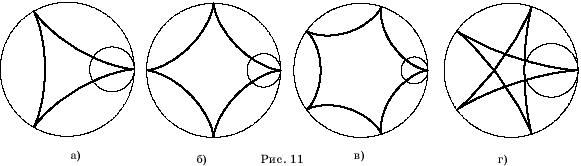
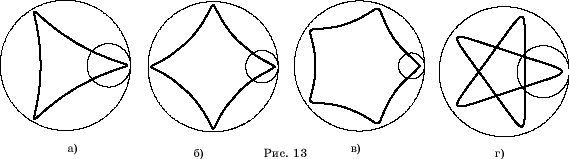
На рисунках
11, а-г показаны гипоциклоиды в случаях, когда отношение радиусов катящейся
и неподвижной окружности равно: а) 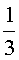 ;
б)
;
б) 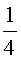 ; в)
; в) 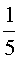 ;
г)
;
г) 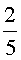 .
.
 На рисунках
12 и 13 показаны соответствующие удлиненные и укороченные гипоциклоиды.
На рисунках
12 и 13 показаны соответствующие удлиненные и укороченные гипоциклоиды.
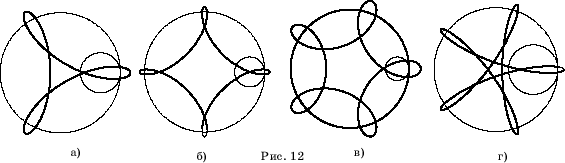
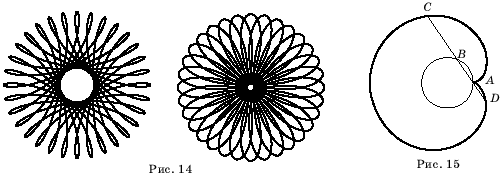
 На рисунке
14 приведены еще два примера гипоциклоид, полученных с помощью компьютера
[2].
На рисунке
14 приведены еще два примера гипоциклоид, полученных с помощью компьютера
[2].
Задачи
1. Докажите,
что касательная к циклоиде перпендикулярна отрезку, соединяющему точку
касания и точку соприкосновения окружности с прямой, по которой она катится.
2. Нарисуйте
траекторию движения вершины правильного n-угольника,
когда он катится по прямой аналогично окружности: а) n =
3; б) n
= 4; в) n = 6.
3. Докажите,
что кардиоида обладает следующим свойством: если провести произвольную
прямую через точку А (рис. 15)
и от точки B ее пересечения
с неподвижной окружностью отложить в обе стороны отрезки равные диаметру
окружности, то концы этих отрезков С и D будут
принадлежать кардиоиде.
4. Нарисуйте
эпициклоиду с отношением радиусов, равным; а) 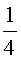 ;
б)
;
б) 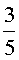 ; в)
; в) 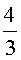 ;
г) 2. Нарисуйте соответствующие удлиненные и укороченные эпициклоиды.
;
г) 2. Нарисуйте соответствующие удлиненные и укороченные эпициклоиды.
5. Нарисуйте
гипоциклоиду с отношением радиусов, равным; а)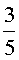 ;
б)
;
б) 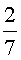 ; в)
; в) 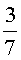 ;
г)
;
г) 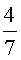 . Нарисуйте соответствующие
удлиненные и укороченные гипоциклоиды.
. Нарисуйте соответствующие
удлиненные и укороченные гипоциклоиды.
6. Докажите,
что если внутри большой окружности катится окружность вдвое меньшего диаметра,
то любая точка внутренней окружности будет двигаться по диаметру внешней
окружности.
ЛИТЕРАТУРА
1. Смирнова
И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных
учреждений. – М.: Просвещение, 2001.
2. Смирнова
И.М., Смирнов В.А. Компьютер помогает геометрии. – М.:
Дрофа, 2003.
3. Березин
В. Кардиоида //Квант. – 1977. № 12.
4. Берман
Г.Н. Циклоида. – М.: Наука, 1975.
5. Васильев
Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич
А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951.
- / Популярные лекции по математике, выпуск 4.
7. Савелов
А.А. Плоские кривые. – М.: Физматлит,
1960.
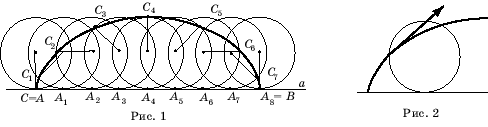
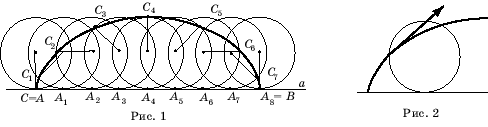










![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ;
г) 2. Нарисуйте соответствующие удлиненные и укороченные эпициклоиды.
;
г) 2. Нарисуйте соответствующие удлиненные и укороченные эпициклоиды.
![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ;
г)
;
г) ![]() . Нарисуйте соответствующие
удлиненные и укороченные гипоциклоиды.
. Нарисуйте соответствующие
удлиненные и укороченные гипоциклоиды.