3.
ЛОМАНЫЕ И МНОГОУГОЛЬНИКИ
Фигура на
плоскости, образованная конечным набором отрезков, расположенными так, что
конец первого является началом второго, конец второго - началом третьего и т.д.
называется ломаной линией или просто ломаной. Отрезки
называются сторонами ломаной, а их концы - вершинами
ломаной.
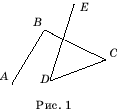
Ломаная обозначается последовательным указанием ее вершин. Например, ломаная АВСDE
(рис. 1).
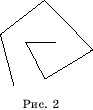
Ломаная называется простой, если она не имеет точек
самопересечения (рис. 2).
Если
начало первого отрезка ломаной совпадает с концом последнего, то ломаная
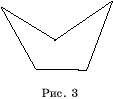
называется замкнутой. Замкнутую ломаную, у которой точками
самопересечения являются только начальная и конечная точки также называют
простой (рис. 3).
Одной
из наиболее важных теорем, относящихся к общим свойствам простых замкнутых
ломаных на плоскости, является следующая теорема Жордана.
Теорема (Жордана). Всякая простая замкнутая ломаная на плоскости разбивает точки
плоскости на две области – внутреннюю и внешнюю. При этом всякие две точки из
одной области могут быть соединены ломаной, целиком содержащейся в этой области,
а две точки из разных областей – нет, т.е. если же две точки принадлежат разным
областям, то любая ломаная, их соединяющая, пересекается с исходной ломаной.
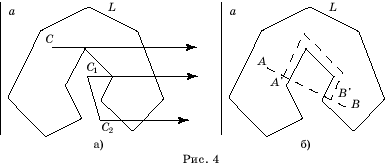
Доказательство. Пусть L – заданная простая замкнутая ломаная (рис. 4). Выберем
на плоскости какую-нибудь прямую a, не перпендикулярную ни одной из
сторон ломаной L. Так как число сторон ломаной конечно, то такая прямая
существует.
Для
точки C плоскости, не принадлежащей ломаной L, рассмотрим луч с
вершиной C, перпендикулярный
a. Заметим, что ни одна из
сторон ломаной не будет целиком лежать на этом луче. Подсчитаем число точек
пересечения этого луча с ломаной L. При этом, если рассматриваемый луч
проходит через вершину ломаной, то эта вершина идет в счет или не идет, в
зависимости от того, расположены ли прилежащие к этой вершине стороны
многоугольника по разные или по одну сторону от данного луча. Если число
пересечений нечетно, то точку C отнесем к внутренней области. Если число
точек пересечения четно, то точку C отнесем к внешней области.
Условимся
говорить, что две точки имеют одинаковую четность, если они обе принадлежат
внутренней области или внешней области.
Заметим,
что если отрезок не пересекается с ломаной, то все его точки имеют одинаковую
четность. Действительно, четность точки движущейся по такому отрезку, может
измениться только при прохождении соответствующего луча через вершину ломаной. Но,
принимая во внимание принятый подсчет точек пересечения, легко видеть, что в
каждом из двух возможных случаев четность не меняется.
Из
сказанного следует, что если какая-нибудь ломаная соединяет две точки разной
четности, то она пересекается с L. Иначе четность всех точек ломаной, а
значит, конечной и начальной точек, была бы одинаковой.
Пусть
A и B – две точки одинаковой четности. Покажем, что их можно
соединить ломаной, не пересекающейся с L. Действительно, если отрезок AB
не пересекается с ломаной, то он является искомой ломаной.
Пусть
отрезок AB пересекается с ломаной. Обозначим A’ и B’ соответственно
первую и последнюю точку пересечения. Построим ломаную, начинающуюся в точке A
и заканчивающуюся в B. Сначала она идет по отрезку AA’. Перед
точкой A’ она поворачивает и идет вдоль ломаной L (безразлично, в
каком из двух возможных направлений) до тех пор, пока снова не пересечет
отрезок AB около точки B’. Выбирая ломаную достаточно близко к
ломаной L, можно добиться, чтобы она не пересекалась с L.
Весь
вопрос в том, кончается ли построенная ломаная на отрезке A’B’ или на
отрезке B’B. Покажем, что первое невозможно.
Действительно,
если две точки расположены близко друг к другу, но по разные стороны от одной
из сторон ломаной L, то они будут иметь разную четность. Следовательно,
точки отрезка A’B’, расположенные близко к B’, не могут быть
соединены ломаной с точкой A, значит, построенная ломаная заканчивается
на отрезке BB’.
Завершим
построение ломаной, соединив отрезком ее последнюю точку с точкой B. В
результате получим искомую ломаную, соединяющую точки A и B.
Фигура
на плоскости, образованная простой замкнутой ломаной и ограниченной ею
внутренней областью, называется многоугольником. Вершины ломаной
называются вершинами многоугольника, стороны ломаной – сторонами многоугольника, а углы, образованные
соседними сторонами – углами многоугольника. Диагональю
многоугольника называется
отрезок, соединяющий две его несоседние вершины.
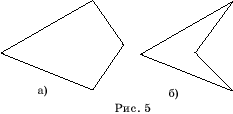
Многоугольник
называется выпуклым, если отрезок, соединяющий любые две его точки,
содержится в этом многоугольнике. На рисунке 5 приведены примеры выпуклых и
невыпуклых многоугольников.
Теорема. В каждом многоугольнике с числом сторон большим трех можно провести
диагональ, целиком в нем содержащуюся.
Доказательство. Заметим, что в выпуклом многоугольнике содержится любая его диагональ.
Для невыпуклого многоугольника некоторые диагонали могут в нем не содержаться.
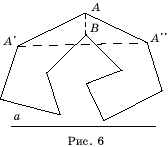
Для нахождения диагонали, целиком содержащейся в данном многоугольника M зафиксируем
какую-нибудь прямую a, и найдем вершину A многоугольника,
расстояние от которой до этой прямой наибольшее. Пусть A’, A’’ –
соседние с ней вершины (рис. 6). Если отрезок A’A’’ целиком содержится в
многоугольнике M, то он является искомой диагональю. Если A’A’’
не содержится целиком в M, то существуют вершины многоугольника M, содержащиеся
в треугольнике A’AA’’. Выберем из них вершину B, наиболее
удаленную от прямой a. Тогда отрезок AB будет целиком содержаться
в многоугольнике и, следовательно, он является искомой диагональю.
Следствие. Любой многоугольник можно разбить на треугольники.
Действительно,
по доказанной теореме, многоугольник можно разбить на два многоугольника,
проведением диагонали. Продолжая процесс проведения диагоналей, мы, в конце
концов, дойдем до треугольников, на которые будет разбит наш многоугольник.
Заметим,
что для n-угольника число таких треугольников будет равно n-2. Докажем это индукцией по n.
Если
n = 4, то число треугольников равно двум, предположим, что для всех m
< n мы доказали, что число
треугольников, на которые разбиваются m-угольник, проведением
диагоналей, равно m – 2.
Рассмотрим
n-угольник, и проведем в нем диагональ. Она разобьет этот n-угольник
на k-угольник и n – k + 2–угольник. По предположению индукции, проведением
диагоналей, k-угольник разбивается на k –2 треугольника, а n– k + 2–угольник разбивается на n – k треугольника. Все вместе они
дают разбиение n-угольника на n – 2 треугольника. Что и
требовалось доказать.
Рассмотрим
теперь вопрос о вычислении суммы углов многоугольников.
В
школьном курсе геометрии доказывается, что сумма углов выпуклого n-угольника
равна (n-2)180![]() . Это
же верно и для невыпуклых n-угольников.
. Это
же верно и для невыпуклых n-угольников.
Теорема. Сумма углов произвольного n-угольника равна (n-2)180![]() .
.
Доказательство. Разобьем n-угольник на треугольники, проведением диагоналей
(рис. 7). Число таких треугольников равно n-2, и в каждом треугольнике
сумма углов равна 180![]() .
Поскольку углы треугольников составляют углы n-угольника, то сумма углов
многоугольника равна (n-2)180
.
Поскольку углы треугольников составляют углы n-угольника, то сумма углов
многоугольника равна (n-2)180![]() .
.
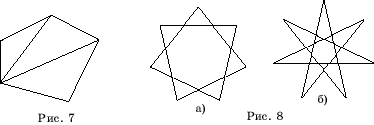
Расширим определение многоугольника, разрешив замкнутой ломаной иметь точки самопересечения. Замкнутые самопересекающиеся ломаные будем называть звездчатыми многоугольниками (рис. 8).
Выясним,
чему равна сумма углов таких многоугольников. Зафиксируем направление подсчета
углов многоугольника (рис. 9). А именно, при переходе от предыдущего звена
ломаной к последующему будем считать угол, образованный этими звеньями, в
направлении против часовой стрелки. Заметим, что если направление изменить на
противоположное, то углами многоугольника будут углы, дополняющие углы исходного
многоугольника до 360![]() .
.
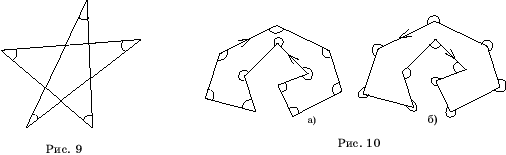
Если
M – многоугольник, образованный простой замкнутой ломаной, проходимой в
направлении по часовой стрелке (рис. 10, а), то сумма углов этого
многоугольника будет равна (n-2)180![]() . Если же ломаная проходится в направлении против
часовой стрелки (рис. 10, б), то сумма углов будет равна (n+2)180
. Если же ломаная проходится в направлении против
часовой стрелки (рис. 10, б), то сумма углов будет равна (n+2)180![]() .
.
Таким
образом, общая формула суммы углов многоугольника, образованного простой
замкнутой ломаной, имеет вид ![]() = (n
= (n![]() 2)180
2)180![]() ,
,
где ![]() - сумма углов, n –
число углов многоугольника, «+» или «-» берется в зависимости от направления
обхода ломаной.
- сумма углов, n –
число углов многоугольника, «+» или «-» берется в зависимости от направления
обхода ломаной.
Наша
задача состоит в том, чтобы вывести формулу суммы углов произвольного
многоугольника, образованного замкнутой (возможно самопересекающейся) ломаной.
Для этого введем понятие степени многоугольника.
Степенью
многоугольника называется число оборотов, совершаемой точкой при полном
последовательном обходе сторон многоугольника. Причем обороты, совершаемые в
направлении против часовой стрелки, считаются со знаком «+», а обороты по
часовой стрелке – со знаком «-».
Ясно,
что у многоугольника, образованного простой замкнутой ломаной, степень равна +1
или –1 в зависимости от направления обхода. Степень звездчатых семиугольников
(рис. 8, а, б) равна соответственно двум и трем.
Аналогичным
образом понятие степени определяется и для замкнутых кривых на плоскости. Для
нахождения степени многоугольника или кривой можно поступать следующим образом.
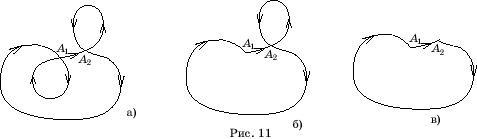
Предположим, что, двигаясь по кривой (рис. 11, а), мы, начиная с какого-то
места A1, совершили полный оборот, и
попали в ту же точку A1.
Удалим из кривой соответствующий участок и продолжим движение по оставшейся
кривой (рис. 11, б). Если, начиная с какого-то места A2, мы снова совершили полный
оборот и попали в ту же точку, то удаляем соответствующий участок кривой и
продолжаем движение (рис. 11, в). Считая количество удаленных участков со
знаками «+» или «-», в зависимости от их направления обхода, получим искомую
степень кривой.
Теорема.
Для произвольного многоугольника имеет место формула
![]() = (n +2m)180
= (n +2m)180![]() , где
, где ![]() - сумма углов, n – число углов,
m – степень многоугольника.
- сумма углов, n – число углов,
m – степень многоугольника.
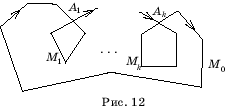
Доказательство. Пусть многоугольник M имеет степень m и условно
изображен на рисунке 12. M1, …, Mk – простые замкнутые ломаные, проходя по
которым, точка совершает полные обороты. A1, …, Ak – соответствующие точки
самопересечения ломаной, не являющиеся ее вершинами.
Обозначим
число вершин многоугольника M, входящих в многоугольники M1, …, Mk через n1, …, nk соответственно. Поскольку,
помимо вершин многоугольника M, к этим многоугольникам добавляются еще
вершины A1,
…, Ak, то число вершин многоугольников M1, …, Mk будет равно соответственно n1+1, …, nk+1. Тогда суммы их углов
будут равны (n1+1![]() 2)180
2)180![]() , …, (nk+1
, …, (nk+1![]() 2)180
2)180![]() . Плюс или минус берется в зависимости от направления обхода
многоугольников.
. Плюс или минус берется в зависимости от направления обхода
многоугольников.
Сумма
углов многоугольника M0, оставшегося от многоугольника M после
удаления многоугольников M1, …, Mk, равна
(n-n1- …-nk+k![]() 2)180
2)180![]() .
.
Суммы
углов многоугольников M0, M1, …, Mk дают сумму ![]() углов многоугольника M и в каждой вершине
A1, …, Ak дополнительно получим 360
углов многоугольника M и в каждой вершине
A1, …, Ak дополнительно получим 360![]() . Следовательно, имеем
равенство
. Следовательно, имеем
равенство
(n1+1![]() 2)180
2)180![]() + …+ (nk+1
+ …+ (nk+1![]() 2)180
2)180![]() +(n-n1- …-nk+k
+(n-n1- …-nk+k![]() 2)180
2)180![]() =
= ![]() +k
+k![]() 360°.
360°.
Приводя подобные члены, получим
![]() =(n
=(n![]() 2
2![]() …
…![]() 2)180
2)180![]() =(n+2m)180
=(n+2m)180![]() ,
,
где m –
степень многоугольника M.
Применяя доказанную формулу для семиугольников (рис.
8, а, б), получаем, что сумма углов семиугольника, изображенного на рисунке 8,
а, равна 3![]() 180
180![]() , а сумма углов семиугольника,
изображенного на рисунке 8, б, равна 180
, а сумма углов семиугольника,
изображенного на рисунке 8, б, равна 180![]() . При этом неважно, правильные это семиугольники
или нет.
. При этом неважно, правильные это семиугольники
или нет.
Литература
1. Адамар Ж. Элементарная геометрия. Часть первая. Планиметрия. – М.: Учпедгиз, 1957.
2. Аргунов Б.И., Балк М.Б. Элементарная геометрия. – М.: Просвещение, 1966, с.70.
3. Коксетер Г.С.М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука, 1978.
4. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1967.
5. Перепелкин Д.И. Курс элементарной геометрии. Часть I. Геометрия на плоскости. – М.-Л.: Гос. изд. техн.-теорет лит., 1948.
6. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Часть 2. Геометрия (планиметрия). - М.: Гос. изд. техн.-теорет лит., 1952.
7. Энциклопедия элементарной геометрии. Книга IV. Геометрия. – М.: Гос. изд. физико-математ. лит., 1963, с.382.