ВЫПУКЛЫЕ МНОГОГРАННИКИ.
ТЕОРЕМА ЭЙЛЕРА
Обычно в школьных курсах геометрии дается следующее определение многогранника.
Определение. Многогранником называется тело, поверхность которого
состоит из конечного числа многоугольников.
При этом понятия тела и поверхности, хотя и имеют наглядный смысл, нуждаются в
уточнении. Причем их строгие определения используют основные понятия топологии:
внутренняя и граничная точка, внутренность и граница, открытость, замкнутость,
связность, ограниченность.
Напомним, что окрестностью Ur(A) точки A
пространства радиуса r называется фигура, стоящая из всех точек
пространства, удаленных от точки A на расстояние, меньшее r.
Таким образом,
Ur(A) = {B| d(A, B)
< r}.
Точка A пространства
называется внутренней точкой фигуры Ф, если у нее
существует окрестность, целиком содержащаяся в этой фигуре.
Точка A пространства называется внешней точкой фигуры Ф,
если у нее существует окрестность, не содержащая точек фигуры Ф, т.е.
целиком лежащая в дополнении к этой фигуре.
Точка A пространства называется граничной точкой фигуры Ф,
если она не является ни внутренней, ни граничной точкой этой фигуры, т.е. в
любой ее окрестности если как точки фигуры Ф, так и точки, не
принадлежащие этой фигуре.
Внутренностью фигуры Ф называется фигура, состоящая из
всех внутренних точек этой фигуры.
Фигура Ф называется открытой, если каждая ее точка
является внутренней или, что то же самое, фигура Ф совпадает со своей
внутренностью.
Границей фигуры Ф называется фигура, состоящая из всех
граничных точек этой фигуры.
Фигура Ф называется замкнутой, если все ее граничные
точки принадлежат Ф.
Фигура Ф называется ограниченной, если она целиком
содержится в некоторой окрестности.
Фигура Ф называется линейно связной, если любые две ее
точки можно соединить кривой, целиком содержащейся в этой фигуре.
Фигура Ф называется выпуклой, если любые две ее точки
можно соединить отрезком, целиком содержащейся в этой фигуре.
Ясно, что выпуклая фигура является линейно связной. Обратное неверно.
Открытая линейно связная фигура называется областью.
Телом называется ограниченная область вместе со своей границей.
Граница тела называется также его поверхностью.
Примерами тел являются куб, параллелепипед, пирамида, шар, цилиндр, конус и др.
Среди общих
свойств фигур нам понадобятся следующие.
Свойство 1. Отрезок, соединяющий
внутреннюю и внешнюю точки фигуры Ф, содержит хотя бы одну граничную
точку этой фигуры.
Доказательство. Пусть A – внутренняя и B – внешняя точка фигуры Ф.
Разделим отрезок AB пополам и рассмотрим его середину C1. Она либо принадлежит Ф,
либо нет. В первом случае возьмем его правую половину C1B, во втором – левую половину
AC1. Разделим полученный отрезок пополам
точкой C2
и, повторив описанную выше процедуру, получим отрезок, левый конец которого
принадлежит фигуре Ф, а правый нет. Повторяя деление отрезков пополам,
получим последовательность отрезков, левые концы которых принадлежат Ф,
а правые – нет. Пусть C – точка пересечения всех этих отрезков. Тогда в любой
ее окрестности имеются как точки, принадлежащие фигуре Ф, так и точки,
не принадлежащие этой фигуре. Следовательно, C – искомая граничная точка
фигуры Ф, принадлежащая отрезку AB.
Свойство 2.
Пересечение
выпуклых фигур является выпуклой фигурой.
Доказательство. Пусть Фa- выпуклые фигуры. Ф = ![]() Фa. Если точки A и B
принадлежат Ф, то они принадлежат каждой фигуре Фa. В силу выпуклости этих
фигур, в них будет содержаться и отрезок AB. Значит он будет содержаться
и в пересечении Ф =
Фa. Если точки A и B
принадлежат Ф, то они принадлежат каждой фигуре Фa. В силу выпуклости этих
фигур, в них будет содержаться и отрезок AB. Значит он будет содержаться
и в пересечении Ф = ![]() Фa.
Фa.
Многогранник называется выпуклым,
если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками
содержит и соединяющий их отрезок.
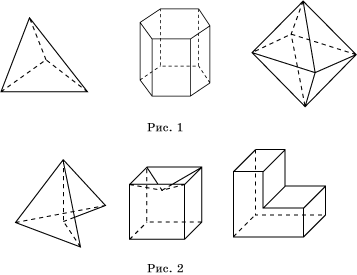
Примеры выпуклых и невыпуклых
многогранников приведены на рисунках 1 и 2, соответственно.
Теорема 1. Все грани выпуклого
многогранника являются выпуклыми многоугольниками.
Действительно, грань многогранника можно представить
как пересечение многогранника и плоскости, содержащей эту грань. После этого
остается только воспользоваться свойством 2.
Заметим, что обратное утверждение неверно.
А именно, из того, что гранями многогранника являются выпуклые многоугольники,
не следует выпуклость самого многогранника. Попробуйте привести примеры таких
многогранников.
Теорема 2. Многогранник является
выпуклым тогда и только тогда, когда он лежит по одну сторону от плоскости
каждой своей грани.
Доказательство. Пусть m – одна из граней выпуклого многогранника M.
Предположим, что точки A и B многогранника лежат по разные
стороны от плоскости этой грани. Соединим эти точки отрезками со всеми точками m.
Получим две пирамиды с вершинами A, B и основанием m. В силу выпуклости
многогранника обе пирамиды содержатся в M. Это противоречит тому, что
грань m состоит из граничных точек многогранника.
Докажем обратное. Пусть многогранник M лежит по одну сторону от
плоскости каждой своей грани. Для каждой такой плоскости a многогранник определяет
полупространство Pa , в котором он находится. Следовательно, имеет
место включение ![]() .
.
Пусть точка B не принадлежит многограннику M. Возьмем
какую-нибудь внутреннюю точку A этого многогранника и соединим ее
отрезком с точкой B. По свойству 1, отрезок AB пересекается с
одной из граней многогранника M. Следовательно, точки A и B
лежат по разные стороны от плоскости a этой грани. Но тогда точка B не
принадлежит полупространству Pa и, значит, не принадлежит пересечению полупространств.
Таким образом, мы доказали, что все точки многогранника принадлежат пересечению
полупространств, и никакая другая точка не принадлежит этому пересечению.
Поэтому имеет место равенство ![]() . Каждое из полупространств является выпуклой
фигурой. Пересечение выпуклых фигур, очевидно, выпуклая фигура. Следовательно, M
– выпуклый многогранник.
. Каждое из полупространств является выпуклой
фигурой. Пересечение выпуклых фигур, очевидно, выпуклая фигура. Следовательно, M
– выпуклый многогранник.
Теорему Эйлера, доказанную Л. Эйлером в 1752 г., историки математики называют
первой теоремой топологии - раздела геометрии, который изучает свойства фигур,
не меняющихся при непрерывных деформациях, допускающих любые растяжения и
сжатия, но без разрывов или дополнительных склеек. Такие свойства называются
топологическими.
Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство
В – Р + Г = 2 (*),
где
В - число вершин, Р - число ребер и Г - число граней данного многогранника.
Соотношение Эйлера В – Р + Г = 2 для выпуклых многогранников является
топологическим свойством. Многогранник можно как угодно деформировать, при этом
ребра и грани могут даже искривляться, однако их число, а следовательно, и
соотношение Эйлера при этом не меняются.
Для доказательства соотношения Эйлера представим поверхность выпуклого
многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его
граней и оставшуюся поверхность растянем на плоскости. Получим сетку,
содержащую Г' = Г – 1 многоугольников (которые, по-прежнему, будем называть
гранями), В вершин и Р ребер.
Для этой сетки, как было показано ранее (в курсе планиметрии), справедливо
соотношение
В - Р + Г ' = 1.
Поэтому
для многогранника справедливо требуемое равенство.
Дадим еще одно доказательство теоремы Эйлера. Рассмотрим какую-нибудь сферу,
содержащую данный многогранник, и из внутренней точки многогранника
спроектируем его поверхность на эту сферу. Образы ребер многогранника образуют
сетку (граф) на сфере. Стянем одно из ребер этой сетки в его вершину. При этом
число вершин и ребер уменьшится на единицу, а В – Р + Г не изменится. Будем
повторять эту операцию для ребер с двумя вершинами. В результате мы придем к
сетке из петель с одной общей вершиной. Будем теперь убирать петли до тех пор,
пока не останется одна петля. При этом каждый раз число вершин не меняется, а
число ребер и граней уменьшается на единицу. Следовательно В – Р + Г не
меняется. Для одной петли на сфере очевидно имеют место равенства В = 1, Р = 1,
Г = 2 и, следовательно, имеем равенство В – Р + Г = 2.
Отметим, что равенство Эйлера выполняется не только для выпуклых многогранников, но и для многогранников, поверхность которых гомеоморфна сфере.
На рисунке 3, а, б изображены многогранники, для которых равенство Эйлера не выполняется.
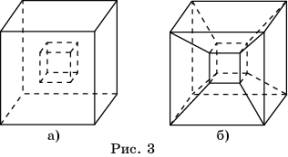
Многогранник на рисунке 3, а получен вырезанием
маленького куба внутри большого куба. Для этого многогранника выполняется
равенство В – Р + Г = 4. Многогранник на рисунке 3, б получен вырезанием в кубе
сквозного прямоугольного отверстия. Для этого многогранника выполняется
равенство В – Р + Г = 0.
Задача. Приведите примеры
невыпуклых многогранников, поверхности которых гомеоморфны сфере.
Задача. Приведите пример многогранника, поверхность которого
не гомеоморфна сфере, но для которого выполняется равенство В – Р + Г = 2.
Рассмотрим несколько следствий теоремы Эйлера о выпуклых многогранниках.
Следствие 1 . В любом выпуклом многограннике имеется или
треугольная грань, или трехгранный угол. Более того, число треугольных граней
плюс число трехгранных углов больше или равно восьми.
Доказательство. Обозначим через Вi число вершин выпуклого многогранника, в которых
сходится i ребер. Тогда для общего числа вершин В имеет место равенство
В = В3 + В4 + В5 + … .
Аналогично, обозначим через Гi число граней выпуклого многогранника, у которых
имеется i ребер. Тогда для общего числа граней Г имеет место равенство Г
= Г3 + Г4 + Г5 + … . Посчитаем число ребер Р
многогранника. Имеем: 3В3
+ 4В4 + 5В5 + … = 2Р, 3Г3 + 4Г4 + 5Г5 + … = 2Р. По теореме Эйлера
выполняется равенство 4В – 4Р + 4Г = 8. Подставляя вместо В, Р и Г их выражения,
получим
4В3 + 4В4
+ 4В5 + … – (3В3
+ 4В4 + 5В5 + …) – (3Г3 + 4Г4 + 5Г5 + …) + 4Г3 + 4Г4
+ 4Г5 + … = 8.
Следовательно, В3
+ Г3 = 8 + В5 + … + Г5 + … , значит, число
треугольных граней плюс число трехгранных углов больше или равно восьми.
Следствие 2. В любом выпуклом многограннике имеется грань с
числом сторон, меньшим шести.
Доказательство. Обозначим через Вi число вершин выпуклого
многогранника, в которых сходится i ребер. Тогда для общего числа вершин
В имеет место равенство В = В3 + В4 + В5 + … . Аналогично, обозначим через Гi число граней выпуклого многогранника,
у которых имеется i ребер. Предположим, что у многогранника нет граней с
числом сторон, меньшим шести. Тогда для общего числа граней Г имеет место
равенство Г = Г6 + Г7 + Г8 + … . Посчитаем
число ребер Р многогранника. Имеем: 3В3 + 4В4 + 5В5 + … = 2Р, 6Г6 + 7Г7 + 8Г8 + … = 2Р. Из этих равенств следует выполнимость
неравенств 3В ![]() 2Р и 6Г
2Р и 6Г ![]() 2Р, из которых получаем: 3В – 3Р + 3Г
2Р, из которых получаем: 3В – 3Р + 3Г ![]() 0, а по теореме
Эйлера должно выполняться равенство 3В – 3Р + 3Г = 6. Полученное противоречие
показывает, что неверным было наше предположение об отсутствии граней с числом
сторон, меньшим шести. Значит, в выпуклом многограннике обязательно найдется
грань с числом сторон, меньшим шести.
0, а по теореме
Эйлера должно выполняться равенство 3В – 3Р + 3Г = 6. Полученное противоречие
показывает, что неверным было наше предположение об отсутствии граней с числом
сторон, меньшим шести. Значит, в выпуклом многограннике обязательно найдется
грань с числом сторон, меньшим шести.
Задача. Докажите, что в любом выпуклом многограннике
имеется многогранный угол с числом ребер, меньшим шести.
Следствие 3. Для любого выпуклого многогранника имеет место формула
![]() 2 = 180
2 = 180![]() (Г – 2 ) +
(Г – 2 ) + ![]() ,
,
где ![]() 2 – сумма двугранных углов,
2 – сумма двугранных углов, ![]() - сумма
многогранных углов этого многогранника.
- сумма
многогранных углов этого многогранника.
Доказательство. Ранее мы доказали, что для многогранного угла SA1…An и его двугранных углов SA1, …, SAn имеет
место формула
![]() SA1 + … +
SA1 + … +![]() SAn= 180
SAn= 180![]() (n
– 2) + 2
(n
– 2) + 2![]() SA1…An
SA1…An
Пусть n1, ..., nв - количества ребер, сходящихся
в вершинах данного многогранника. Тогда, суммируя соответствующие равенства по
всем вершинам многогранника, и учитывая, что при этом каждый двугранный угол
считается дважды, получим равенство
2![]() 2 = 180
2 = 180![]() (n1
– 2) + ... + 180
(n1
– 2) + ... + 180![]() (nв – 2) + 2
(nв – 2) + 2![]() ,
,
где ![]() 2,
2, ![]() - суммы двугранных и многогранных
углов данного многогранника.
- суммы двугранных и многогранных
углов данного многогранника.
Заметим, что n1
+ ... + nв
= 2Р. Следовательно, будем иметь равенство
![]() 2 = 180
2 = 180![]() (Р – В) +
(Р – В) + ![]() ,
,
или,
окончательно
![]() 2 = 180
2 = 180![]() (Г – 2 ) +
(Г – 2 ) + ![]() .
.
Еще
одной важной теоремой о выпуклых многогранниках является теорема Коши,
доказанная им в 1813 г. и называемая теоремой о жесткости выпуклого
многогранника. Она утверждает, что если два выпуклых многогранника, имеют
соответственно равные грани, составленные одинаковым образом, то эти
многогранники равны. При этом, слова «составленные одинаковым образом»
означают, что если две грани одного многогранника имеют общее ребро, то и
соответствующие им грани другого многогранника также имеют общее ребро.
Доказательство
этой теоремы можно, например, найти в книгах [2], [3].
Для
невыпуклых многогранников указанное в теореме Коши свойство перестает быть
верным.
Задача. Приведите примеры двух
неравных многогранников, имеющих соответственно равные грани, составленные
одинаковым образом.
Литература
1. Адамар Ж.
Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Александров
А.Д. Выпуклые многогранники. – М.-Л.; 1950.
3. Долбилин
Н.П. Жемчужины теории многогранников. – М.: МЦНМО, 2000, с.27-31.
4. Люстерник
Л.А. Выпуклые фигуры и многогранники. – М.; 1956, с.69.
5. Перепелкин
Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.:
Гостехиздат, 1949.
6. Смирнова
И.М. В мире многогранников. – М.: Просвещение, 1995.
7. Шклярский
Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной
математики. Часть 3. Геометрия (Стереометрия). – М.; 1954, с.15, с.18
/Библиотека математического кружка, выпуск 3.
8. Энциклопедия
элементарной математики. Книга IV. Геометрия. - М.; 1963.
9. Яглом И.М.,
Болтянский В.Г. Выпуклые фигуры. – М.-Л.; 1951 /Библиотека математического
кружка, выпуск 4.