ВПИСАННЫЕ И
ОПИСАННЫЕ МНОГОУГОЛЬНИКИ
Тема
«Вписанные и описанные многоугольники» является одной из основных в курсе
геометрии 7-9 классов. Однако ее изучение ограничивается вписанными и
описанными треугольниками и правильными многоугольниками.
В новых стандартах
по математике профильного уровня обучения в курсе геометрии 10-11 классов
предусматривается изучение вписанных и описанных четырехугольников, в
частности, необходимых и достаточных условий вписанности и описанности, теоремы
Птолемея и др.
Здесь мы предлагаем материал о вписанных
и описанных многоугольниках, который можно использовать при углубленном
изучении математики, проведении элективных курсов, подготовки школьников к
различным турнирам, конкурсам и олимпиадам по математике.
Начнем с рассмотрения некоторых свойств
вписанных четырехугольников. В отличие от треугольников, не около каждого
четырехугольника можно описать окружность. Нетрудно доказать, что имеет место
следующая теорема.
Теорема
1. Если четырехугольник вписан в
окружность, то сумма его противоположных углов равна 180о.
Действительно, например, углы A и C вписанного
в окружность четырехугольника ABCD опираются на дуги, в сумме составляющие всю
окружность. Поскольку вписанный угол измеряется половиной дуги, на которую он
опирается, сумма углов A и C равна 180о.
Верно и обратное утверждение, а именно.
Теорема
2. Если сумма противоположных углов
четырехугольника равна 180о, то около него можно описать окружность.
Действительно, пусть ABCD –
четырехугольник, у которого сумма углов A и C равна 180о.
Заметим, что геометрическое место точек C, из которых отрезок BD виден под углом 180о - ÐA,
представляет собой дугу окружности, стягиваемую хордой BD. Так как
по условию ÐA + ÐC = 180о,
то точка C должна принадлежать данной окружности.
Таким образом, имеет место следующая
теорема.
Теорема
3. Около четырехугольника можно
описать окружность тогда и только тогда, когда сумма его противоположных углов
равна 180о.
В качестве применения этой теоремы
предлагаем несколько задач.
Задача 1. Можно ли описать
окружность около: а) прямоугольника; б) параллелограмма; в) ромба; г) квадрата;
д) равнобедренной трапеции; е) прямоугольной трапеции?
Ответ. а), г), д) Да;
б), в) е) нет.
Задача 2. Можно ли описать окружность около четырехугольника, углы
которого последовательно равны: а) 70о, 130о, 110о, 50о; б) 90о, 90о, 60о, 120о; в) 45о, 75о, 135о, 105о; г) 40о, 125о, 55о, 140о?
Ответ. а), в) Да; б), г)
нет.
Задача 3. Два угла вписанного в окружность четырехугольника равны
80о и 60о.
Найдите два других угла четырехугольника.
Ответ. 100о и 120о.
Задача 4. Углы A, B и C четырехугольника ABCD относятся как 2:3:4. Найдите
угол D, если
около данного четырехугольника можно описать окружность.
Ответ. 90о.
Выясним, каким условиям должны удовлетворять
стороны четырехугольника, вписанного в окружность.
Пусть четырехугольник ABCD со сторонами a, b, c, d вписан в окружность. По теореме
косинусов
AC2 = a2 + b2 – 2abcosj = c2 + d2 – 2cdcos(180оj) = c2
+ d2 + 2cdcosj.
Откуда
cos j = 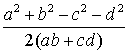
и, следовательно, должно
выполняться неравенство
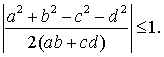
Верно
и обратное, если для сторон четырехугольника выполняется указанное неравенство,
то мы можем определить угол j, положив
j = arccos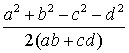 .
.
Полученное неравенство эквивалентно
неравенству
|a2 + b2 – c2 – d2|![]() 2(ab + cd)
2(ab + cd)
и,
значит, системе неравенств
-2(ab + cd) ![]() a2 + b2 – c2 – d2
a2 + b2 – c2 – d2![]() 2(ab + cd)
2(ab + cd)
Сделаем несколько равносильных
преобразований этой системы.
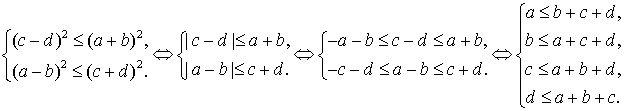
Легко
видеть, что последняя система неравенств справедлива для любого
четырехугольника со сторонами a, b, c, d. Таким образом, имеет место
следующая теорема.
Теорема
4. Для произвольного четырехугольника ABCD
существует четырехугольник A’B’C’D’ с такими же сторонами, около
которого можно описать окружность.
В качестве применения этой теоремы
предлагаем несколько задач.
Задача
5. Можно ли описать окружность около четырехугольника со
сторонами 1 см, 2 см, 3 см, 4 см?
Более точная формулировка: существует
ли четырехугольник со сторонами 1 см, 2 см, 3 см, 4 см, около которого можно
описать окружность?
Ответ. Да.
Задача
6. Можно ли описать окружность около четырехугольника со сторонами 1 см, 2
см, 3 см, 4 см и одной диагональю 4 см.
Ответ. Нет.
Задача
7. Стороны вписанного в окружность четырехугольника ABCD равны a, b, c, d. Найдите его диагонали.
Ответ.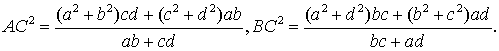
Теорема Птолемея для четырехугольника,
вписанного в окружность, утверждает, что произведение его диагоналей равно сумме
произведений противоположных сторон. Мы докажем более сильную теорему.
Теорема
5. Произведение диагоналей
произвольного четырехугольника меньше или равно сумме произведений его
противоположных сторон, причем равенство достигается только в случае четырехугольника,
вписанного в окружность.
Доказательство. Пусть ABCD –
четырехугольник. Воспользуемся инверсией с центром в точке A и радиусом
R.
Напомним, что при инверсии точкам X, отличным от A, сопоставляются точки X’ на луче AX, для которых ![]() При этом окружности,
не проходящие через точку A, переходят в окружности, а окружности, проходящие
через точку A, за исключением самой точки A, переходят
в прямые.
При этом окружности,
не проходящие через точку A, переходят в окружности, а окружности, проходящие
через точку A, за исключением самой точки A, переходят
в прямые.
Пусть
точки B, C и D переходят соответственно в точки B’, C’ и D’. Тогда
треугольники ABC и A’C’B’, ADC и AC’D’, ABD и AD’B’ подобны и,
следовательно, имеют место равенства
![]()
Складывая почленно эти равенства, получим
![]()
Следовательно, имеет место неравенство ![]() При этом, равенство
достигается только в случае, когда точки B’, C’, D’ принадлежат одной прямой. Это выполняется только в
случае, если точки B, C, D принадлежат
окружности, проходящей через точку A.
При этом, равенство
достигается только в случае, когда точки B’, C’, D’ принадлежат одной прямой. Это выполняется только в
случае, если точки B, C, D принадлежат
окружности, проходящей через точку A.
Рассмотрим
теперь пятиугольники, вписанные в окружность. Начнем с задачи.
Задача 8. Можно ли описать окружность
около пятиугольника с углами 80о,
90о, 100о, 130о, 140о?
Для ее
решения установим соотношение между углами вписанного пятиугольника. Заметим,
что углы A и C опираются на дуги, в сумме составляющие всю
окружность плюс дугу DE. Из этого вытекает следующая теорема.
Теорема 6. Сумма любых двух несоседних
углов вписанного пятиугольника больше 180о.
Указанные
в задаче 8 углы не удовлетворяют этому условию, и, значит, около такого
пятиугольника нельзя описать окружность.
Естественный
вопрос, который возникает после этого – является полученное условие
достаточным, чтобы около пятиугольника можно было описать окружность?
Ответ:
Нет.
Пример
такого пятиугольника легко построить. Возьмем какой-нибудь вписанный
пятиугольник ABCDE и, продолжая две его стороны, построим пятиугольник ABCD’E’ так, чтобы сторона D’E’ была
параллельна DE. Тогда углы этого пятиугольника будут равны углам
исходного, и около него нельзя описать окружность.
Поставим
другой вопрос, связанный с достаточным условием вписанности пятиугольника.
Пусть ABCDE –
пятиугольник, сумма любых двух несоседних углов которого больше 180о. Существует ли пятиугольник A’B’C’D’E’ с такими
же углами, около которого можно описать окружность?
Прежде
чем ответить на этот вопрос решим следующую задачу.
Задача 9. По данным углам вписанного
пятиугольника ABCDE найдите углы между его диагоналями, выходящими из
одной вершины.
Ответ. ÐCAD = ÐB + ÐE - 180о. Аналогичным
образом выражаются и другие углы.
Вернемся
теперь к поставленному вопросу. Для ответа на него рассмотрим какую-нибудь
окружность и разделим ее на дуги, равные углам между диагоналями исходного
пятиугольника, выходящим из одной вершины. Концы этих дуг будут вершинами
искомого пятиугольника вписанного в окружность.
Таким
образом, имеет место следующая теорема.
Теорема 7. Для произвольного
пятиугольника ABCDE, суммы любых двух несоседних углов которого больше
180о, существует
пятиугольник A’B’C’D’E’ с такими же
углами, около которого можно описать окружность.
Задача 10. По радиусу окружности и
углам вписанного в нее пятиугольника ABCDE найдите
стороны этого пятиугольника.
Ответ. AB = 2RsinÐADB =
-2Rsin(ÐC+ÐE). Аналогичным образом выражаются другие стороны
пятиугольника.
Задача 11. По радиусу окружности и
сторонам вписанного в нее пятиугольника найдите углы этого пятиугольника.
Ответ. ÐA = arcsin![]() + arcsin
+ arcsin![]() + arcsin
+ arcsin![]() . Аналогичным образом
выражаются другие углы пятиугольника.
. Аналогичным образом
выражаются другие углы пятиугольника.
Решение
задачи 10 показывает, что для пятиугольника, вписанного в окружность, имеет
место теорема, аналогичная теореме синусов для треугольника.
Теорема 8. Для пятиугольника ABCDE,
вписанного в окружность радиуса R имеют место равенства.
(*)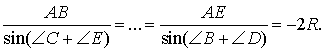
Оказывается
верно и обратное утверждение.
Теорема 9. Если для пятиугольника ABCDE выполняются равенства (*), то
около него можно описать окружность радиуса R.
Для
доказательства рассмотрим окружность радиуса R и
отложим на ней дуги, равные удвоенным величинам ÐB + ÐE -
180о, … . Концы этих
дуг будут вершинами многоугольника, равного исходному.
Следующая
теорема дает ответ на вопрос о том, можно ли описать окружность около
пятиугольника с данными сторонами.
Теорема 10. Для произвольного
пятиугольника ABCDE существует пятиугольник A’B’C’D’E’ с такими же сторонами, около которого можно описать
окружность.
Доказательство.
Пусть, стороны пятиугольника равны a, b, c, d, e, где e – его наибольшая сторона. Если при R = e/2 выполняется равенство
![]()
то, откладывая на окружности радиуса R дуги
величины
![]()
получим, что концы этих дуг являются вершинами
искомого пятиугольника. Предположим, что при R = e/2
выполняется неравенство
![]()
Тогда при увеличении R левая часть уменьшается и стремится к нулю. Поэтому
найдется R, при котором будет выполняться равенство
![]()
и, значит, существует искомый пятиугольник.
Предположим, что при R = e/2 выполняется неравенство
![]()
или, что то же самое, неравенство
![]()
Докажем, что найдется R, для которого будет выполняться равенство
![]()
Для окружности радиуса R=e/2 отложим
хорды A’B’ = a, B’C’ = b, C’D’=c, D’E’ = d. Тогда будет выполняться неравенство A’E’ < e. При стремлении радиуса окружности к ![]() хорда A’E’ будет стремиться к a + b + c + d. Поскольку
e <
a + b + c + d, то найдется R, при котором будет выполняться требуемое равенство.
Соответствующий пятиугольник A’B’C’D’E’ будет искомым пятиугольником, вписанным в окружность.
хорда A’E’ будет стремиться к a + b + c + d. Поскольку
e <
a + b + c + d, то найдется R, при котором будет выполняться требуемое равенство.
Соответствующий пятиугольник A’B’C’D’E’ будет искомым пятиугольником, вписанным в окружность.
Эта
теорема дает ответ на следующую задачу.
Задача 12. Можно ли описать окружность
около пятиугольника со сторонами 1, 2, 3, 4, 5?
Более
точная формулировка: существует ли пятиугольник со сторонами 1, 2, 3, 4, 5,
около которого можно описать окружность.
Ответ.
Да.
Ситуация
с вписанными в окружность семиугольниками, девятиугольниками и т. д. аналогична
рассмотренной ситуации с пятиугольниками. В частности, имеют место следующие
теоремы.
Теорема11. Сумма любых трех несоседних
углов вписанного семиугольника больше 360о.
Теорема 12. Для произвольного
семиугольника ABCDEFG, суммы любых трех несоседних углов которого больше
360о, существует
семиугольник A’B’C’D’E’F’G’ с такими же
углами, около которого можно описать окружность.
Теорема
13. Для семиугольника ABCDEFG,
вписанного в окружность радиуса R имеют
место равенства.
(**) 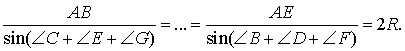
Теорема 14. Если для семиугольника ABCDE
выполняются равенства (**), то около него можно описать окружность радиуса R.
Теорема 15. Для произвольного
семиугольника ABCDEFG существует семиугольник A’B’C’D’E’F’G’ с такими же сторонами, около которого можно описать
окружность.
Для
вписанных многоугольников с четным числом сторон ситуация аналогична ситуации с
вписанным четырехугольником. В частности, для вписанного шестиугольника имеют
место следующие теоремы.
Теорема 16. Сумма трех несоседних углов
вписанного шестиугольника равна 360о.
Теорема 17. Если сумма трех несоседних
углов выпуклого шестиугольника равна 360о, то существует шестиугольник с такими же углами, около
которого можно описать окружность.
Заметим,
что в отличие от вписанного пятиугольника, углы вписанного шестиугольника и
радиус описанной окружности определяют стороны шестиугольника неоднозначно.
Действительно, рассмотрим какой-нибудь вписанный шестиугольник ABCDE.
Повернем треугольник BDF вокруг центра окружности на некоторый угол. Получим
треугольник B’D’F’. Шестиугольник AB’CD’EF’ будет вписанным и иметь те же углы, что и данный
шестиугольник.
Задача 13. Можно ли описать окружность
около шестиугольника с углами 100о,
110о, 120о, 120о, 130о, 140о?
Ответ.
Нет.
Задача 14. Четыре последовательных угла
вписанного шестиугольника равны 100о,
110о, 120о, 120о. Найдите оставшиеся два угла.
Ответ.
140о и 130о.
Задача 15. По углам вписанного
шестиугольника ABCDEF найдите угол
между диагоналями AC и AE.
Ответ.
180о - ÐD.
Перейдем
теперь к рассмотрению описанных многоугольников. Ситуация здесь в некотором
смысле двойственная по отношению к вписанным многоугольникам. При этом стороны
описанного многоугольника двойственны углам вписанного многоугольника. Так,
например, если для вписанности четырехугольника необходимым и достаточным
условием является равенство сумм противоположных углов, то для описанности
выпуклого четырехугольника необходимым и достаточным условием является
равенство сумм противоположных сторон. А именно, имеют место следующие
теоремы.
Теорема 18. Суммы противоположных
сторон описанного около окружности четырехугольника равны.
Доказательство.
Пусть четырехугольник ABCD описан около окружности, A’, B’, C’, D’ – точки касания. Тогда AA’ = AD’, BA’ = BB’, DC’ = DD’, CC’ = CB’. Складывая почленно эти равенства, получим равенство AB + CD = AD + BC, означающее, что суммы противоположных сторон
вписанного четырехугольника равны.
Теорема 19. Если суммы противоположных
сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Доказательство.
Пусть в выпуклом четырехугольнике ABCD имеет место равенство AB + CD = BC + AD.
Рассмотрим окружность, касающуюся сторон углов A и D. Центром этой окружности является точка пересечения
биссектрис углов A и D. Предположим, что эта окружность не касается стороны BC. Проведем
касательную B’C’, для
которой угол B’ равен углу B. Тогда четырехугольник AB’C’D будет описан около окружности и, следовательно, для
него будет выполняться равенство AB’ + C’D = AD + B’C’. С другой
стороны, по условию, выполняется равенство AB + CD = AD + BC. Вычитая
из первого равенства второе, получим равенство BB’ +CC’ = B’C’ – BC, или B’C’ = BB’ + BC + CC’. Последнее равенство не может выполняться для точек
не лежащих на одной прямой и, значит, неверным было наше предположение о том,
что окружность не касается стороны BC.
Самостоятельно
подумайте, где в доказательстве использовалась выпуклость четырехугольника.
Приведите пример невыпуклого четырехугольника, у которого суммы противоположных
сторон равны и в который нельзя вписать окружность.
В
качестве применения этих теорем предлагаем следующие задачи.
Задача 16. Можно
ли вписать окружность в: а) прямоугольник; б) параллелограмм; в) ромб; г)
квадрат; д) дельтоид?
Ответ. а), б) Нет; в), г), д) да.
Задача
17. Можно ли вписать окружность в четырехугольник со
сторонами 1, 2, 3, 4?
Ответ. Нет.
Задача
18. Три последовательные стороны четырехугольника, в который
можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и
периметр этого четырехугольника.
Ответ. Сторона - 7 см, периметр – 30 см.
Задача 19. Противоположные стороны четырехугольника, описанного
около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр
четырехугольника?
Ответ. Да, периметр
равен 34 см.
Выясним, каким условиям должны
удовлетворять углы четырехугольника, чтобы в него можно было вписать
окружность.
Конечно, описанный четырехугольник
должен быть выпуклым. Это равносильно тому, что углы четырехугольника меньше
180о. Докажем, что имеет место следующая теорема.
Теорема
20. Для произвольного выпуклого четырехугольника ABCD существует четырехугольник A’B’C’D’ с
такими же углами, в который можно вписать окружность.
Действительно,
зафиксируем R и рассмотрим восемь прямоугольных треугольников с катетом R и противолежащим острым
углом A/2, A/2, B/2, B/2, C/2, C/2, D/2, D/2.
Складывая эти треугольники, получим четырехугольник A’B’C’D’, в который можно вписать
окружность и углы которого равны
углам исходного четырехугольника.
Задача 20. Можно ли вписать окружность
в четырехугольник с углами 70о,
80о, 100о, 110о?
Ответ.
Да.
Следующие
задачи и теоремы, двойственные соответствующим задачам и теоремам для вписанных
пятиугольников, предлагаем для самостоятельного решения и доказательства.
Задача 21. Можно ли вписать окружность в
пятиугольник со сторонами 1, 2, 1, 2, 1?
Ответ.
Нет.
Теорема 21. Сумма любых двух несоседних сторон описанного пятиугольника
меньше суммы трех оставшихся сторон.
Теорема 22. Для произвольного
пятиугольника ABCDE, сумма любых двух несоседних сторон которого меньше
суммы оставшихся сторон, существует пятиугольник A’B’C’D’E’ с такими же
сторонами, в который можно вписать окружность.
Задача 21. По радиусу окружности и
сторонам описанного около нее пятиугольника найдите его углы.
Задача 22. По радиусу окружности и углам описанного около нее
пятиугольника найдите его стороны.
Теорема 23. Для пятиугольника ABCDE,
описанного около окружности, радиуса R имеют место равенства
(***) 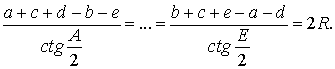
Теорема 24. Если для пятиугольника ABCDE
выполняются равенства (***), то в него можно вписать окружность радиуса R.
Теорема 25. Для произвольного выпуклого
пятиугольника существует пятиугольник с такими же углами, в который можно
вписать окружность.
Задача 23. Можно ли вписать окружность
в пятиугольник с углами 80о,
100о, 110о, 120о, 130о?
Ответ.
Да.
Задача
24. Сформулируйте и докажите теоремы, двойственные теоремам для вписанных
семиугольников и шестиугольников.
Сформулируем
общие теоремы о вписанных и описанных многоугольниках. Их доказательства
повторяют доказательства рассмотренных выше частных случаев.
Теорема I. Сумма любых n
несоседних углов вписанного (2n+1)-угольника больше 180о
(n-1).
Теорема II. Если сумма любых n несоседних углов (2n+1)-угольника
больше 180о (n-1), то существует (2n+1)-угольник
с такими же углами, около которого можно описать окружность.
Теорема III. Сумма n несоседних углов вписанного 2n-угольника
равна 180о (n-1).
Теорема IV. Если
сумма n несоседних углов 2n-угольника
равна 180о (n-1), то существует 2n-угольник
с такими же углами, около которого можно описать окружность.
Теорема V. Сумма любых n
несоседних сторон описанного (2n+1)-угольника меньше суммы его
остальных сторон.
Теорема VI. Если сумма любых n несоседних сторон (2n+1)-угольника
меньше суммы его остальных сторон, то существует (2n+1)-угольник
с такими же сторонами, в который можно вписать окружность.
Теорема VII. Сумма n несоседних сторон описанного 2n-угольника
равна сумме его остальных сторон.
Теорема VIII. Если
сумма n несоседних сторон 2n-угольника
равна сумме его остальных сторон, то существует 2n-угольник
с такими же сторонами, в который можно вписать окружность.