ФИГУРНЫЕ ЧИСЛА
Фигурные числа использовались еще в V – IV веках до н. э. Древнегреческие
математики предпочитали думать о числах, как о геометрических величинах.
Произведение ab рассматривалось как площадь прямоугольника со сторонами a
и b. В случае, если a и b – натуральные, произведение ab
выражало число точек в прямоугольной таблице с a точками в строке и b
точками в столбце. Например, число 20 выражает число точек в таблице с пятью
строками и четырьмя столбцами (рис. 1). Такие числа назывались прямоугольными.
Числа, выражающие число точек в квадратной таблице, назывались квадратными.
Например, квадратными числами являются 1, 4, 9, 16, … (рис. 2).

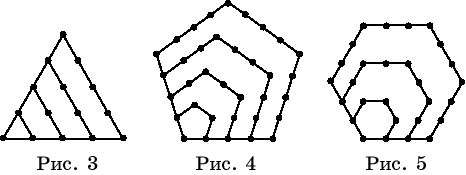
Таблицы могут быть не только прямоугольными или квадратными, но и иметь форму
других геометрических фигур. Например, на рисунке 3 изображены треугольные
числа, выражающие числа точек в треугольных таблицах. На рисунках 4 и 5
изображены пятиугольные и шестиугольные числа. Из этих рисунков видно, что
пятиугольными числами являются 1, 5, 12, 22, 35, … , а шестиугольными – 1, 6,
15, 28, 45, … .
Для
того чтобы вывести формулу n-го d-угольного числа, рассмотрим
последовательность 1, 1 + (d – 2),
1 + 2(d – 2), 1 + 3(d – 2), … 1 + (n – 1)(d – 2), … ,
представляющую собой арифметическую прогрессию с начальным членом 1 и
знаменателем d– 2. Нетрудно видеть, что n-е d-угольное число ![]() является суммой первых n членов этой прогрессии и, следовательно,
выражается формулой
является суммой первых n членов этой прогрессии и, следовательно,
выражается формулой
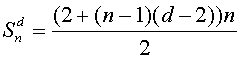 .
.
Фигурное
представление чисел помогает найти различные числовые закономерности. Так,
например, рассмотрим n2 точек, расположенных в
квадрате, как показано на рисунке 6 для n = 5.
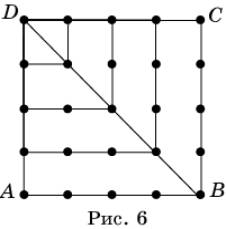
Треугольник DAB содержит точки, образующие
треугольное число, равное 1 + 2 + … + n. Треугольник DBC также
содержит точки, образующие треугольное число, равное 1 + 2 + … + n.
Общая сторона DB этих треугольников содержит n точек.
Следовательно, имеет место равенство
2(1
+ 2 + … + n) – n = n2,
из которого получаем равенство
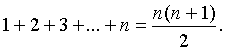
Если
считать точки этого квадрата, группируя их по уголкам, идущим с левой верхней
до правой верхней точки, то получим равенство
1 + 3 + 5 + … + (2n –
1) = n2.
Между
фигурными числами имеется много интересных зависимостей. Так, например,
древнегреческий математик Диофант (III век до н. э.) нашел зависимость между
треугольными (Т) и квадратными (К) числами: 8Т + 1 = К.
Проиллюстрируем
доказательство Диофанта на примере треугольного числа Т3 = 6. На рисунке 7
изображены 49 точек, образующих квадратное число К7.
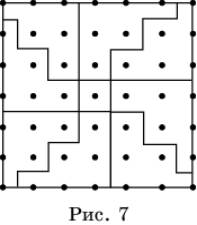
Выделим
среди этих точек центральную, а остальные точки разобьем на группы, образующие
восемь треугольных чисел Т3. В результате получаем
равенство 8Т3 + 1 = К7. В общем случае имеет место равенство 8Tn + 1 = K2n+1.
Пьер Ферма (1601 – 1655) обнаружил, что всякое натуральное число есть
треугольное, или сумма двух или трех треугольных чисел.
Французский математик О. Коши в 1815 г. доказал, что
всякое натуральное число может быть представлено в виде суммы не более чем d d-угольных чисел.
Для отдельных случаев это утверждение было доказано
Л. Эйлером (1707-1783).
Фигурные числа можно образовывать, используя и пространственные фигуры.
Например, кубические числа 1, 8, 27, … представляют собой число точек в
кубических таблицах (рис. 8), пирамидальные числа 1, 4, 10, … представляют
число точек в треугольных пирамидах (рис. 9), пирамидальные числа 1, 5, 14, …
представляют число точек в четырехугольных пирамидах (рис. 10).
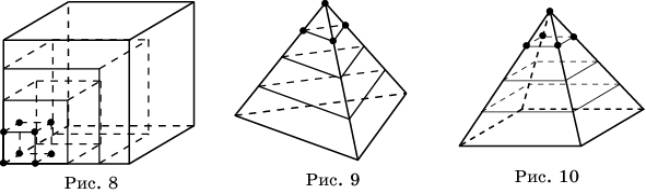
Пространственные фигурные числа можно получать, составляя последовательные
суммы из плоских фигурных чисел V1 = S1, V2 = S1 + S2, V3 = S1 + S2 + S3, V4 = S1 + S2 + S3 + S4 и т. д.
Так, ряд треугольных чисел 1, 3, 6, 10, 15, … производит следующий ряд
пирамидальных чисел: 1, 4, 10, 20, 35, … .
Английский
математик XVIII в. Э. Варинг поставил задачу о разложении натуральных
чисел в сумму кубических чисел и чисел больших степеней. Было доказано, что
всякое натуральное число можно представить в виде суммы не более девяти
кубических чисел. В общем случае проблема Варинга остается открытой.
Пространственные
фигурные числа можно использовать для нахождения различных формул для сумм
чисел. Воспользуемся пирамидальными числами для нахождения формулы для суммы 12
+ 22 + … + n2.
Рассмотрим
куб OABCO1A1B1C1 в координатном пространстве (рис. 11).
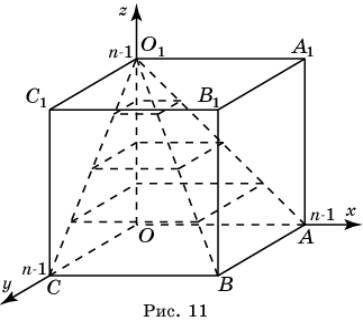
Число
точек этого куба с целыми координатами равно n3.
Разобьем куб на три пирамиды O1OABC, O1ABB1A1 и O1BCC1B1. Число точек пирамиды O1OABC с целыми
координатами, расположенных в плоскостях z = n-1, z = n-2,
…, z = 0, равно
соответственно 1, …, n2. Общее число точек этой пирамиды O1OABC с целыми
координатами равно 12 + 22 + … + n2. В
пирамидах O1ABB1A1 и O1BCC1B1 число точек с целыми координатами также равно 12
+ 22 + … + n2.
Пирамиды
O1OABC и O1ABB1A1 имеют общую
грань O1AB, число точек которой с целыми координатами равно 1 +
2 + … + n = ![]() Аналогично, пирамиды O1OABC,
O1BCC1B1 и O1ABB1A1, O1BCC1B1 имеют
общие грани соответственно O1BC и
O1BB1, в каждой из которых число точек с целыми координатами
равно
Аналогично, пирамиды O1OABC,
O1BCC1B1 и O1ABB1A1, O1BCC1B1 имеют
общие грани соответственно O1BC и
O1BB1, в каждой из которых число точек с целыми координатами
равно ![]()
Все три пирамиды O1OABC, O1ABB1A1 и O1BCC1B1 имеют общее ребро O1B, число точек в котором с целыми координатами равно n. Суммируя точки с целыми координатами во всех трех пирамидах, получаем равенство
![]() из которого следует равенство
из которого следует равенство
![]()
Аналогичным образом,
рассматривая разбиение четырехмерного куба на четыре гиперпирамиды, можно
получить следующее равенство
![]() из которого следует равенство
из которого следует равенство
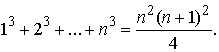
В
общем случае имеет место равенство
![]()
которое позволяет находить сумму 1m + 2m + … + nm через суммы
меньших степеней.
В частности, имеет место формула
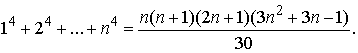
Рассмотрим
числа, связанные с фигурными числами, образующие равнобедренный треугольник,
называемый треугольником Паскаля. По боковым сторонам этого треугольника стоят единицы и всякое число, кроме этих единиц,
получается как сумма двух чисел, расположенных над данным числом.
Таблица 1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
……………..
Блез Паскаль посвятил этому треугольнику "Трактат об арифметическом
треугольнике", опубликованный в 1653 г. В нем этот треугольник записывался
в виде таблицы
Таблица 2
1 1 1 1 1 1
1 2 3 4 5
1 3 6 10
1 4 10
1 5
1
в которой каждое
число равно сумме чисел, расположенных слева и сверху над ним. Будем называть
его прямоугольным треугольником Паскаля. Таким образом, треугольник Паскаля
отличается от прямоугольного треугольника, рассматривавшегося самим Паскалем,
поворотом на 45°.
В действительности треугольник Паскаля был известен задолго до Паскаля.
Итальянский математик Николо Тарталья в книге "Общий трактат о числе и
мере (1556 – 1560 гг.) рассмотрел прямоугольник
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
3 |
6 |
10 |
15 |
21 |
|
1 |
4 |
10 |
20 |
35 |
56 |
|
1 |
5 |
15 |
35 |
70 |
126 |
|
1 |
6 |
21 |
56 |
126 |
252 |
в котором верхняя
строка и левый столбец состоят из единиц, а каждое оставшееся число равно сумме
чисел, расположенных слева и сверху над ним. Омар Хайям, бывший не только поэтом
и философом, но и математиком, знал о треугольнике Паскаля (около 1100 г), в
свою очередь, заимствовав его из более ранних китайских или индийских
источников.
Несмотря на свою простоту, треугольник Паскаля обладает целым рядом интересных
свойств. Упомянем некоторые из них.
1. Треугольник Паскаля симметричен относительно высоты.
2. Каждое число в прямоугольном треугольнике Паскаля равно сумме чисел
предшествующей строки, начиная с первого до числа, стоящего непосредственно над
данным числом.
3. Каждое число в прямоугольном треугольнике Паскаля, будучи уменьшено на 1,
равно сумме чисел, заполняющих прямоугольник, ограниченный строкой и столбцом,
на которых стоит данное число.
4. Третья строка и третий столбец прямоугольного треугольника Паскаля состоят
из треугольных чисел.
5. Четвертая строка и четвертый столбец прямоугольного треугольника Паскаля
состоят из пирамидальных чисел.
6. Сумма чисел n-ой строки треугольника Паскаля равна 2n, так как при переходе от
каждой строки к следующей сумма чисел удваивается, а для нулевой строки она
равна 1.
Обозначим через ![]() число,
стоящее на k-ом месте в n-ой строке треугольника Паскаля, начиная
с нулевого места и нулевой строки. По определению, имеет место равенство
число,
стоящее на k-ом месте в n-ой строке треугольника Паскаля, начиная
с нулевого места и нулевой строки. По определению, имеет место равенство ![]()
Выясним связь между числами треугольника Паскаля и биномиальными
коэффициентами.
Биномиальными коэффициентами называются коэффициенты при x, получающиеся
при возведении бинома 1 + x в степень n ³ 0.
Имеем
(1 + x)0 = 1;
(1 + x)1 = 1 + x;
(1 + x)2 = (1 + x)(1 + x)
= 1 + 2x + x2;
(1 + x)3 = (1 + x)2(1 + x) = 1 + 3x
+ 3x2 + x3;
……………………………………………..
Обозначим через ![]() коэффициент при xk в разложении (1 + x)n. Из приведенных выше
разложений можно предположить, что имеет место равенство
коэффициент при xk в разложении (1 + x)n. Из приведенных выше
разложений можно предположить, что имеет место равенство ![]() =
= ![]() . Действительно,
по определению имеет место равенство
. Действительно,
по определению имеет место равенство
![]()
Найдем разложение для (1+x)n+1, представляя его в виде (1+x)n(1+x).
Имеем
![]()
![]()
Учитывая, что коэффициент при xk+1 в последней сумме по определению равен ![]() ,
получаем формулу
,
получаем формулу ![]() Сравнивая
ее с формулой для чисел треугольника Паскаля, видим, что биномиальные
коэффициенты и числа треугольника Паскаля получаются по тому же закону и,
следовательно, имеет место равенство
Сравнивая
ее с формулой для чисел треугольника Паскаля, видим, что биномиальные
коэффициенты и числа треугольника Паскаля получаются по тому же закону и,
следовательно, имеет место равенство ![]() =
= ![]() .
.
Докажем, что для чисел треугольника Паскаля, а значит, и для биномиальных
коэффициентов имеет место формула
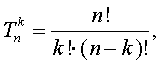
где
n! (читается эн факториал) равно
произведению чисел 1, 2, …, n, и 0! считается равным единице.
Заметим, что приведенная формула имеет место в случае k = 0 и k = n. В общем случае достаточно
проверить, что выполняется соотношение
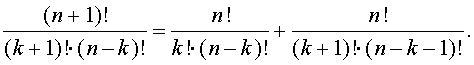
Это
делается непосредственно.
Самостоятельно
решите следующие задачи:
1.
Сколько нечетных чисел в
256-ой строке треугольника Паскаля?
2.
Сколько чисел в 67-ой
строке треугольника Паскаля делится на 67?
3. Прямоугольник n x m
разбит сеткой на единичные квадраты.
Сколькими способами можно пройти по линиям этой сетки из вершины A в
вершину B, если из каждой ее вершины
можно идти или направо, или вверх?
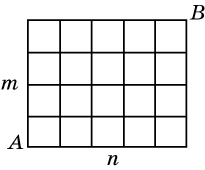
4. Имеется сеть дорог, изображенная на
рисунке. Из точки A
выходит 21000 человек. Одна
половина из них идет направо, а вторая – налево. Дойдя до первого перекрестка,
каждая группа разделяется: одна половина
идет направо, а вторая – налево. Такое же разделение происходит на
каждом перекрестке. Сколько человек придет в три крайних слева перекрестка В1,
В2, В3 тысячного ряда перекрестков?
5. Докажите, что имеет место равенство
![]()
6. Найдите, чему равна сумма
![]()
5. В треугольнике
1
1 1 1
1 2 3
2 1
1 3 6
7 6 3 1
1 4 10 16
19 16 10 4 1
…………….
каждое
число равно сумме трех ближайших к нему чисел предыдущей строки. В n-ой строке будут стоять 2n+1 чисел, которые мы обозначим ![]() Докажите, что
выполняются равенства:
Докажите, что
выполняются равенства:
а) ![]()
б) ![]()
Выясните
алгебраический смысл этих чисел. Найдите для них формулы.
6. Определите аналог треугольника Паскаля в
пространстве (тетраэдр Паскаля). Выясните его алгебраический смысл. Найдите
формулу для его элементов.
Литература
1. Диофант. Арифметика и книга о многоугольных числах. – М.: Наука, 1974.
2.
Гарднер М. Математические новеллы. – М.: Мир, 1974.
3. Кордемский Б.А. Математическая смекалка.- М.: Наука, 1991.
4. Оре О. Приглашение в теорию чисел. – М.: Наука, 1980.
5. Радемахер Г., Теплиц О. Числа и фигуры. – М.: Наука, 1966.
6. Успенский В.А. Треугольник Паскаля. – М.: Наука, 1979.
7.
Яглом А.М., Яглом И.М. Неэлементарные задачи в элементарном изложении. – М.:
Гос. изд. технико-теоретической литературы, 1954.