ТЕОРЕМА ЭЙЛЕРА
Следующая теорема была доказана Леонардом
Эйлером в 1752 году и положила начало нескольким направлениям в математике:
теории графов, топологии и др.
Теорема.
Если многоугольник разбит на конечное число многоугольников так, что любые
два многоугольника разбиения или не имеют общих точек, или имеют общие
вершины, или имеют общие ребра, то имеет место равенство
В - Р + Г = 1, (*)
где В - общее число вершин,
Р - общее число сторон (ребер), Г - число многоугольников (граней).
Доказательство.
Докажем, что соотношение (*) не изменится, если в каком-нибудь многоугольнике
данного разбиения провести диагональ (рис. 1, а). Действительно,
после проведения такой диагонали в новом
разбиении будет В вершин, Р+1 ребер и количество многоугольников увеличится
на единицу. Следовательно, имеем
В - (Р + 1) + (Г+1)
= В – Р + Г.
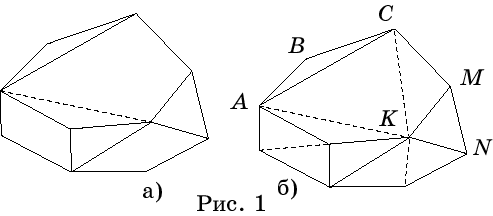 Пользуясь
этим свойством, проведем диагонали, разбивающие входящие многоугольники
на треугольники, и для полученного разбиения покажем выполнимость соотношения
(*) (рис. 1, б). Для этого будем последовательно убирать внешние ребра,
уменьшая количество треугольников. При этом возможны два случая:
Пользуясь
этим свойством, проведем диагонали, разбивающие входящие многоугольники
на треугольники, и для полученного разбиения покажем выполнимость соотношения
(*) (рис. 1, б). Для этого будем последовательно убирать внешние ребра,
уменьшая количество треугольников. При этом возможны два случая:
а) для
удаления треугольника ABC требуется
снять два ребра, в нашем случае AB
и BC;
б) для
удаления треугольника MKN требуется
снять одно ребро, в нашем случае MN.
В обоих
случаях соотношение (*) не изменится. Например, в первом случае после удаления
треугольника граф будет состоять из В-1 вершин, Р-2 ребер и Г-1 многоугольника:
(В - 1) - (Р + 2) +
(Г -1) = В – Р + Г.
Самостоятельно
рассмотрите второй случай.
Таким
образом, удаление одного треугольника не меняет соотношение (*). Продолжая
этот процесс удаления треугольников, в конце концов, мы придем к разбиению,
состоящему из одного треугольника. Для такого разбиения В = 3, Р = 3, Г
= 1 и, следовательно, B - Р + Г= 1.
Значит, соотношение (*) имеет место и для исходного разбиения, откуда окончательно
получаем, что для данного разбиения многоугольника справедливо соотношение
(*).
Заметим,
что соотношение Эйлера не зависит от формы многоугольников. Многоугольники
можно деформировать, увеличивать, уменьшать или даже искривлять их стороны,
лишь бы при этом не происходило разрывов сторон. Соотношение Эйлера при
этом не изменится.
В качестве
приложения теоремы Эйлера рассмотрим задачу о трех домиках и трех колодцах,
также связанную с именем Эйлера.
Задача.
Три соседа имеют три общих колодца. Можно ли провести непересекающиеся
дорожки от каждого дома к каждому колодцу (рис. 2)?
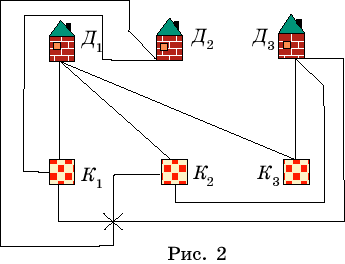 Решение.
Предположим, что это можно сделать. Отметим домики точками Д1,
Д2,
Д3,
а колодцы - точками К1,
К2,
К3
(рис. 2). Каждую точку-домик соединим с каждой точкой-колодцем. Получим
девять ребер, которые попарно не пересекаются.
Решение.
Предположим, что это можно сделать. Отметим домики точками Д1,
Д2,
Д3,
а колодцы - точками К1,
К2,
К3
(рис. 2). Каждую точку-домик соединим с каждой точкой-колодцем. Получим
девять ребер, которые попарно не пересекаются.
Эти ребра
образуют на плоскости многоугольник, разделенный на более мелкие многоугольники.
Поэтому для этого разбиения должно выполняться соотношение Эйлера В - Р
+ Г= 1. Добавим к рассматриваемым граням еще одну - внешнюю часть плоскости
по отношению к многоугольнику. Тогда соотношение Эйлера примет вид В -
Р + Г = 2, причем, В = 6 и Р = 9. Следовательно, Г = 5. Каждая из пяти
граней имеет, по крайней мере, четыре ребра, поскольку, по условию задачи,
ни одна из дорожек не должна непосредственно соединять два дома или два
колодца. Так как каждое ребро принадлежит ровно двум граням, то количество
ребер должно быть не меньше 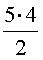 = 10, что противоречит условию, по которому их число равно 9. Полученное
противоречие показывает, что ответ в задаче отрицателен - нельзя провести
непересекающиеся дорожки от каждого домика к каждому колодцу.
= 10, что противоречит условию, по которому их число равно 9. Полученное
противоречие показывает, что ответ в задаче отрицателен - нельзя провести
непересекающиеся дорожки от каждого домика к каждому колодцу.
Литература
1. Адамар Ж. Элементарная
геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Долбилин Н.П. Жемчужины
теории многогранников. – М.: МЦНМО, 2000, с.27-31.
3. Перепелкин Д.И. Курс
элементарной геометрии. Часть II. Геометрия
в пространстве. – М.-Л.: Гостехиздат, 1949, с.273 (с.276 - § 4).
4. Смирновой И.М. В мире
многогранников. – М.: Просвещение, 1995.
5. Шклярский Д.О., Ченцов
Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Часть
3. Геометрия (Стереометрия). – М.; 1954, с.15, с.18 /Библиотека математического
кружка, выпуск 3.
6. Энциклопедия элементарной
математики. Книга IV. Геометрия. -
М.: 1963.
7. Яглом И.М., Болтянский
В.Г. Выпуклые фигуры. – М.-Л.; 1951 /Библиотека математического кружка,
выпуск 4.


