ПОСТРОЕНИЕ ЦИРКУЛЕМ И
ЛИНЕЙКОЙ
Построение циркулем и линейкой занимает важное место в школьном курсе
геометрии. Среди задач на построение отметим следующие:
а) деление отрезка пополам и построение серединного перпендикуляра к отрезку;
б) построение биссектрисы угла;
в) проведение прямой, проходящей через данную точку и перпендикулярную данной
прямой;
г) проведение прямой, проходящей через данную точку и параллельную данной
прямой;
д) построение касательной к окружности, проходящей через данную точку;
е) построение треугольника по его элементам;
ж) построение правильных многоугольников, вписанных и описанных около данной
окружности и др.
Здесь мы рассмотрим вопрос о том, какие задачи на построение выполнимы с
помощью циркуля и линейки, а какие - нет.
Построение циркулем и линейкой предполагает возможность выполнения следующих
операций:
1. Проведение прямой через две данные точки.
2. Проведение окружности с центром в данной точке и данным радиусом.
В результате этих операций к точкам данной совокупности можно присоединять:
а) точку пересечения двух прямых, полученных в результате операции 1;
б) точки пересечения прямой и окружности, полученных в результате операций 1 и
2:
в) точки пересечения двух окружностей, полученных в результате операции 2.
Выясним, какие точки можно построить циркулем и линейкой, исходя из данной
совокупности точек A0, A1, … .
С помощью циркуля и линейки построим оси координат так, чтобы A0 было началом координат, а
отрезок A0A1 – единичным отрезком на оси
абсцисс.
Каждой точке A на плоскости можно сопоставить ее координаты (x,
y). Ясно, что точку A можно построить тогда и только тогда, когда
можно построить ее координаты.
Переходя от точек плоскости к их координатам, выясним, какие числа можно
построить, исходя из данной совокупности действительных чисел.
Для совокупности X действительных чисел
обозначим через Q[X] числа, полученные из чисел
совокупности X применением (возможно многократным) к ним операций
сложения, вычитания, умножения и деления.
Простым квадратичным расширением Q1[X] множества Q[X]
назовем совокупность чисел вида a + b
, где a, b – произвольные
числа множества Q[X], а c –
некоторое фиксированное число множества Q[X] такое, что не принадлежит Q[X]. Легко видеть, что Q[X]
содержится в Q1[X], и сумма, разность,
произведение и частное чисел множества Q1[X] снова принадлежит
множеству Q1[X]. Через Q2[X] обозначим простое
квадратичное расширение множества Q1[X], …, через Qn+1[X]
обозначим простое квадратичное расширение множества Qn[X]. Наконец, квадратичным
расширением Q*[X] множества Q[X]
назовем объединение всех Qn[X]. Квадратичное расширение Q*[X]
можно рассматривать, как множество чисел, получаемых из чисел совокупности X,
применением (возможно многократным) к ним операций сложения, вычитания,
умножения, деления и извлечения квадратного корня.
Теорема 1. Число c можно построить исходя из
данной совокупности X действительных чисел тогда и
только тогда, когда оно выражается через них с помощью операций сложения,
вычитания, умножения, деления и извлечения квадратного корня, т.е. принадлежит
квадратичному расширению Q*[X].
Доказательство. Покажем достаточность. Если числа a и b можно построить,
то можно построить и числа a + b, a – b, a
b, a/b (рис. 1).
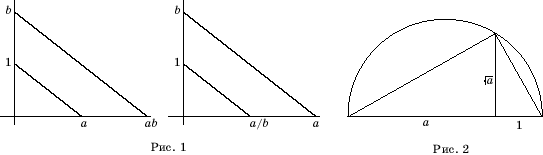
Далее,
если число c > 0 можно построить, то можно построить и число 
(рис. 2). Следовательно,
любое число, получающееся из чисел данной совокупности с помощью операций
сложения, вычитания, умножения, деления и извлечения квадратного корня, можно
построить. Для краткости, будем в дальнейшем называть такие операции
квадратичными.
Покажем необходимость, а именно, что получающиеся при построении с помощью
циркуля и линейки действительные числа, выражаются через данные числа с помощью
квадратичных операций.
1. Пусть точка A(x, y) получена как пересечение двух прямых, проходящих
через точки A1(x1, y1), A2(x2, y2) и A3(x3, y3), A4(x4, y4), координаты которых принадлежат
данной совокупности.
Тогда координаты точки A удовлетворяют системе линейных уравнений
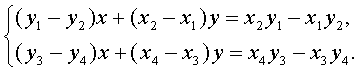
Переобозначив
коэффициенты, перепишем эту систему в виде
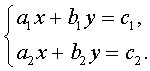
Откуда
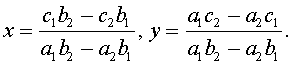
Следовательно,
координаты x и y выражаются через координаты точек A1, A2, A3 и A4 с помощью операций
сложения, вычитания, умножения и деления, входящих в квадратичные операции.
2. Пусть точка A(x, y) получена как пересечение прямой, проходящей через
данные точки A1(x1, y1), A(x2, y2), и окружности с центром в
данной точке A(x3, y3) и радиусом r. При этом координаты данных
точек и радиус принадлежат данной совокупности.
Тогда координаты точки A удовлетворяют системе уравнений
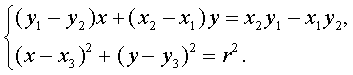
Переобозначив
коэффициенты, перепишем эту систему в виде
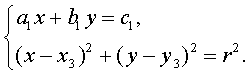
Выразим x или y из первого уравнения и подставим во второе.
Получим квадратное уравнение, коэффициенты которого выражаются через координаты
данных точек с помощью операций сложения, вычитания, умножения и деления. Тогда
корни этого уравнения выражаются с помощью этих же операций и операции
извлечения квадратного корня, т. е. квадратичных операций.
3. Пусть точка A(x, y) получена как пересечение двух
окружностей, проходящей через данные точки A1(x1, y1), A(x2, y2), и данными радиусами r1, r2. При этом координаты данных
точек и радиусы принадлежат данной совокупности.
Тогда координаты точки A удовлетворяют системе уравнений
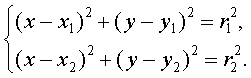
Вычтем из первого уравнения второе. Получим линейное уравнение
2(x2 – x1)x + 2(y2 – y1)y = r12 – r22 – x12 – y12 + x22 + y22.
Добавим к нему второе уравнение. Получим систему, аналогичную системе из
второго случая. Поэтому ее решения выражаются через числа данной совокупности с
помощью квадратичных операций. Что и завершает доказательство.
Рассмотрим некоторые классические задачи на построение.
I. Задача удвоения куба. Она состоит в построении куба, имеющего объем вдвое
больший данного. Точнее, для данного единичного отрезка требуется построить
ребро куба, имеющего объем, равный двум.
Длина ребра искомого куба является действительным корнем кубического уравнения x3– 2 = 0. Поэтому
для ответа на вопрос: можно или нельзя выполнить построение циркулем и
линейкой, нужно ответить на вопрос: выражается или нет число 
с помощью квадратичных
операций, применяемых к числу 1.
II. Задача о трисекции угла состоит в делении произвольного угла на три
равные части.
Конечно, некоторые углы, например, угол, равный 90
можно разделить на три равные части с
помощью циркуля и линейки. Рассмотрим вопрос о возможности такого деления
произвольного угла 
.
Используя тригонометрические формулы, нетрудно получить уравнение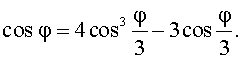 
Следовательно, число 
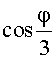является корнем уравнения
4x3
– 3x – cos =
0.
В
частности, если = 60 получаем уравнение 8x3 – 6x – 1 = 0, которое
заменой 2x на y можно привести к виду y3 – 3y – 1 = 0.
Таким образом, ответ на вопрос о возможности деления угла в 60 на три равные части сводится
к вопросу о возможности выражения действительного корня этого уравнения с
помощью квадратичных операций, применяемых к числу 1.
Эти две задачи приводят к необходимости исследования корней кубического
уравнения.
Теорема 2. Если
уравнение x3
+ px2 + qx + r = 0 с коэффициентами из поля Q не имеет корней в поле P.
то оно не имеет корней и в его простом квадратичном расширении.
Доказательство. Пусть число a + b является корнем данного уравнения, где a, b, c принадлежат
P, не принадлежит P. Заметим, что a
+ bявляется
корнем квадратного уравнения (x –(a + b))(x – (a – b)) = 0,
которое можно переписать в виде x2 + Ax + B = 0, где A и B принадлежат P.
Разделим исходное уравнение на полученное квадратное уравнение с остатком.
Получим равенство x3 + px2 + qx + r =( x2 + Ax + B)(x + p – A) + Cx + D,
в
котором все коэффициенты принадлежат P. Так как число a + bявляется корнем
кубического и квадратного уравнения то должно выполняться равенство C(a
+ b) + D = 0,
из которого следует, что a + b принадлежит P.
Значит, b = 0 и a является корнем данного
уравнения.
Противоречие.
Следствие. Если уравнение x3 + px2 + qx + r = 0 с рациональными коэффициентами не имеет рациональных
корней, то его корни не выражаются с помощью квадратичных операций, применяемых
к числу 1.
Заметим, что всякий рациональный корень уравнения x3 + px2 + qx + r = 0 с целыми коэффициентами
является целым числом и делителем свободного члена.
Действительно, пусть 
(m и n взаимно просты) является корнем
кубического уравнения. Тогда имеет место равенство
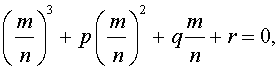
или
m3 + pm2n + qmn2 + rn3 = 0.
Из последнего равенства следует, что r
делится на m и m делится на n. Но m и n
взаимно просты, значит n = 1.
Полученные выше уравнения x3 – 2 = 0 и y3 – 3y – 1 = 0, как легко
видеть, не имеют рациональных корней и, следовательно, их корни не выражаются с
помощью квадратичных операций. Поэтому, задачи об удвоении куба и трисекции
угла неразрешимы.
Рассмотрим еще примеры неразрешимых задач на построение циркулем и линейкой.
III. Задача о квадратуре круга состоит в построении квадрата,
равновеликого данному кругу.
Она неразрешима с помощью циркуля и линейки, так как сводится к построению
числа 
, которое
не только не выражается с помощью квадратичных операций, но является
трансцендентным ( не алгебраическим) числом.
IV. Задача о построении правильных многоугольников, вписанных в
единичную окружность.
Пусть дана окружность единичного радиуса. С помощью циркуля и линейки можно
вписать в эту окружность правильные треугольник, шестиугольник и т. д. 32n-угольник (рис. 3).
Аналогично, в единичную окружность можно вписать правильные 22n-угольники (рис. 4),
правильные 52n-угольники (рис. 5).
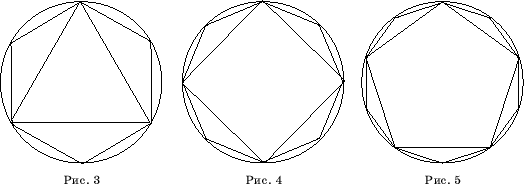
Полностью вопрос о возможности построений правильных многоугольников с помощью
циркуля и линейки был исследован Гауссом. А именно, он доказал, что правильный n-угольник
может быть построен с помощью циркуля и линейки тогда и только тогда, когда n
представимо в виде произведения степени двойки и различных простых чисел
Ферма, т.е. простых чисел вида 
. В частности, из этого следует, что правильный семиугольник
нельзя построить циркулем и линейкой. Докажем это отдельно с использованием
комплексных чисел.
Вершины правильного семиугольника в комплексной плоскости, вписанного в
единичную окружность, являются корнями уравнения z7 - 1 = 0. Один из корней
есть z = 1, а остальные удовлетворяют уравнению z6 + z5 + z4 + z3 + z2 + z + 1 = 0. Деля на
z3, получим уравнение
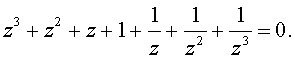
Простые алгебраические преобразования приводят его к виду
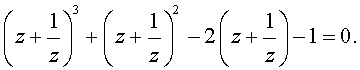
Положив
теперь z + 1/z=t, окончательно приходим к уравнению
t3 + t2 - 2t - 1 = 0 (*).
Так
как комплексное число z представляется в виде z = cos
+ i sin, то 1/z = cos - i sin и, следовательно, t = 2cos является действительным числом.
Как легко видеть, уравнение (*) не имеет рациональных корней и, следовательно,
его корни не выражаются с помощью квадратичных операций.
Таким образом, задача построения правильного семиугольника циркулем и линейкой
неразрешима.
Литература
1. Адамар Ж. Элементарная геометрия. Часть I. – М.: Просвещение, 1957.
2. Адлер А. Теория геометрических построений. – Л.: Учпедгиз, 1940.
3. Александров И.И. Сборник геометрических
задач на построение. – М.: Учпедгиз, 1950.
4.
Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости. – М.: Учпедгиз,
1957.
5. Воронец А.М. Геометрия циркуля.
Ленинград, 1934.
6.
Клейн Ф. Элементарная математика с точки зрения высшей. – М.: Наука, 1987.
7. Костовский А.Н. Геометрические
построения одним циркулем. – М.: Наука, 1984.
8. Перепелкин Д.И. Геометрические построения в средней школе. – М.: Учпедгиз,
1953.
9. Смогоржевский А.С. Линейка в
геометрических построениях. – М., 1957.
10.
Энциклопедия элементарной математики. Т. IV. – М.: Физматлит, 1963.
