ТЕОРЕМЫ МЕНЕЛАЯ, ЧЕВЫ,
ВАН-ОБЕЛЯ
Рассмотрим общие теоремы, позволяющие устанавливать, в каком случае три точки,
лежащие на сторонах треугольника или их продолжениях, принадлежат одной прямой (теорема
Менелая), а также, в каком случае три прямые, проходящие через вершины
треугольника и противоположные им стороны треугольника, пересекаются в одной
точке (теорема Чевы).
Начнем с теоремы Менелая, доказанной древнегреческим математиком и астрономом
Менелаем Александрийским, жившим в I веке до нашей эры.
Теорема (Менелая). Пусть на сторонах AB, BC и продолжении стороны AC
треугольника ABC взяты соответственно точки C1, A1 и B1. Точки A1, B1, C1 лежат на одной прямой тогда
и только тогда, когда выполняется равенство
(*) 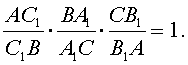
Доказательство. Необходимость. Предположим, что точки A1, B1, C1 принадлежат одной прямой a
(рис. 1).
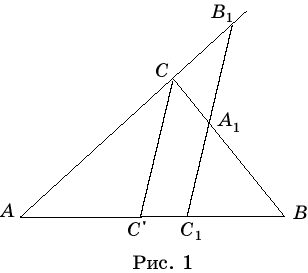
Через вершину C треугольника ABC проведем прямую, параллельную a и обозначим
через C' точку ее пересечения с AB. Из подобия треугольников AC'C
и AC1B следует выполнимость
равенства
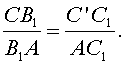
Аналогично,
из подобия треугольников BC'C и BC1A1следует выполнимость
равенства
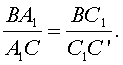
Перемножая
эти равенства, получим равенство
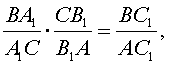
из
которого следует требуемое равенство.
Приведем еще один способ доказательства необходимости.
Предположим, что точки A1, B1, C1 принадлежат одной прямой a.
Из вершин треугольника ABC опустим на эту прямую
перпендикуляры AA’, BB’, CC’
(рис. 2).
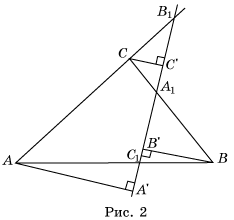
Из подобия треугольников AC1A’
и BC1B’ следует равенство 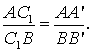 Аналогично, из
подобия треугольников BA1B’
и CA1C’, B1CC’
и B1AA’ следуют равенства
Аналогично, из
подобия треугольников BA1B’
и CA1C’, B1CC’
и B1AA’ следуют равенства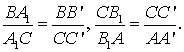 Перемножая все три эти равенства, получим требуемое
равенство (*).
Перемножая все три эти равенства, получим требуемое
равенство (*).
Достаточность. Пусть на сторонах AB, BC и
продолжении стороны AC треугольника ABC взяты соответственно
точки C1, A1и B1, для которых выполняется
равенство (*). Прямая A1B1пересекает прямую AB в точке C'. По
доказанному, выполняется равенство
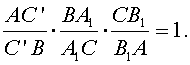
Учитывая
равенство (*), получаем равенство
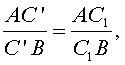
из
которого следует совпадение точек C' и C1. Значит, точки A1, B1, C1 принадлежат одной прямой.
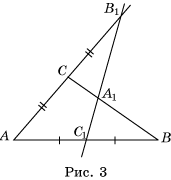
Пример 1. Точка C1 – середина стороны AB
треугольника ABC (рис. 3). Точка B1 лежит на продолжении
стороны AC и AC = CB1. В каком отношении делит
прямая B1C1 сторону BC?
Решение. По условию, 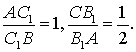 Используя теорему
Менелая, находим
Используя теорему
Менелая, находим 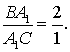
Пример 2.
Докажем, что отрезки, соединяющие вершины тетраэдра с центроидами
противоположных граней, пересекаются в одной точке, называемой центроидом
тетраэдра, и делятся в ней в отношении 3:1, считая от вершин.
Доказательство. Действительно, пусть ABCD – тетраэдр, A2, D2 –
центроиды соответствующих граней, A1 – середина BC, O –
точка пересечения AA2 и DD2 (рис. 4).
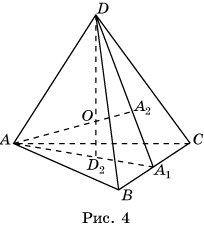
Применим
теорему Менелая к треугольнику A1DD2 и
прямой AA2.
Имеем
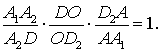
Так как A2 –
точка пересечения медиан треугольника BCD, то 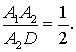 Так как D2 –
точка пересечения медиан треугольника ABC, то
Так как D2 –
точка пересечения медиан треугольника ABC, то 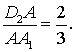 Поэтому
Поэтому 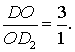
Заметим, что в таком же отношении делят
отрезок DD2
прямые BB2 и CC2.
Следовательно, они также проходят через точку O и делятся в ней в отношении 3:1, считая от вершин.
Задача 1. Докажите, что если прямая пересекает стороны A1A2, …, AnA1
замкнутой
ломаной A1…An или их продолжения в точках B1, …, Bn, соответственно, то имеет место равенство 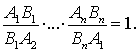
Задача 2. Докажите, что точки A1, B1, C1, D1, лежащие на ребрах AB, BC, CD и DA
тетраэдра ABCD, принадлежат одной плоскости тогда и только тогда,
когда выполняется равенство 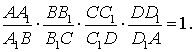
Рассмотрим теперь теорему, опубликованную в 1678 году
итальянским математиком и инженером Джованни Чевой.
Теорема (Чевы). Пусть на сторонах AB, BC и AC треугольника ABC
взяты соответственно точки C1, A1
и B1. Прямые AA1, BB1, CC1 пересекаются в одной точке
тогда и только тогда, когда
(*)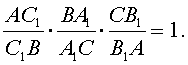
Доказательство. Необходимость. Предположим, что прямые AA1, BB1, CC1 пересекаются в точке O (рис.
5).
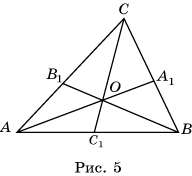
Применим
теорему Менелая к треугольнику BCC1 и прямой AA1. получим равенство 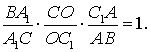 Аналогично, применяя
теорему Менелая к треугольнику ACC1 и прямой BB1, получим равенство
Аналогично, применяя
теорему Менелая к треугольнику ACC1 и прямой BB1, получим равенство 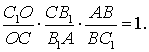 Перемножая эти два
равенства, получим требуемое равенство.
Перемножая эти два
равенства, получим требуемое равенство.
Предложим еще один способ
доказательства теоремы Чевы, использующий понятие площади. Предположим, что прямые AA1, BB1, CC1 пересекаются в точке O (рис. 6).
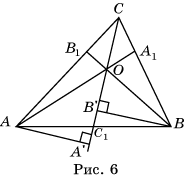
Опустим
из вершин A и B треугольника ABC перпендикуляры
AA’, BB’ на
прямую CC1.
Треугольники AC1A’ и BC1B’ подобны
и, следовательно,
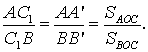
Аналогичным образом
показывается, что
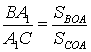 и
и 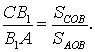
Перемножая полученные равенства, будем иметь
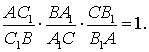
Достаточность. Пусть для точек A1, B1, C1, взятых на соответствующих
сторонах треугольника ABC выполняется равенство (*). Обозначим точку
пересечения прямых AA1 и BB1через O и точку пересечения прямых CO и
AB через C'. Тогда, на основании доказанного, имеет место
равенство
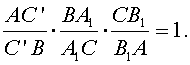
Учитывая
равенство (*), получим равенство
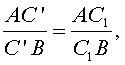
из
которого следует совпадение точек C' и C1и, значит, прямые AA1, BB1, CC1 пересекаются в одной точке.
Заметим, что из этой теоремы непосредственно следует, что медианы треугольника
пересекаются в одной точке.
Воспользуемся теоремой Чевы для установления еще одной замечательной точки
треугольника.
Пример 3.
Докажем, что прямые, проходящие через вершины треугольника и точки касания
вписанной окружности пересекаются в одной точке, называемой точкой Жергона.
Доказательство. Пусть окружность касается сторон треугольника ABC соответственно
в точках A1,
B1,C1 (рис. 7).
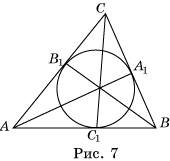
Тогда AB1 = AC1, BC1 = BA1, CA1 = CB1. Следовательно,
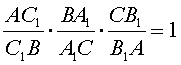
и,
значит, прямые AA1, BB1, CC1 пересекаются в одной точке.
Задача 3. Докажите, что прямые, проходящие через вершины
треугольника и точки касания вневписанных окружностей, пересекаются в одной
точке (точка Нагеля). Окружность
называется вневписанной в треугольник, если она касается одной стороны этого
треугольника и продолжений двух других его сторон.
Задача 4. Докажите следующую теорему.
Теорема (Ван-Обеля). Пусть на сторонах AB, BC
и AC треугольника ABC взяты соответственно точки C1, A1 и B1 (рис. 5). Если отрезки AA1, BB1, CC1 пересекаются в одной точке O,
то
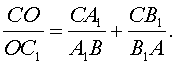
Задача 5. Используя теорему Ван-Обеля, выясните, в каком
отношении делятся биссектрисы треугольника ABC (AB = c, AC = b, BC = a)
точкой их пересечения.
Теорема Стюарта. Пусть в треугольнике ABC AB = c, AC = b, BC = a. Точка D делит сторону AB на
отрезки AD = c’, DB = c” и CD = d.
Тогда имеет место равенство d2c = a2c’ + b2c” – cc’c”.
Доказательство. Пусть СE – высота треугольника ABC (рис.
8).
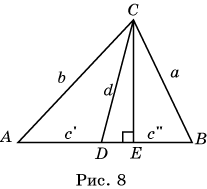
По теореме косинусов, примененной к
треугольникам ADC и BDC, имеем
b2 = (c’)2
+ d2 – 2c’DE, a2
= (c”)2 + d2 – 2c”DE.
Умножим первое равенство на c”,
второе – на c’ и
сложим. Получим b2c” + a2c’ = (c’+c”)c’c” + d2(c’+c”), из которого и следует требуемое равенство.
Пример 4. Используя теорему Стюарта,
вычислим биссектрису CC1 = ![]() треугольника
по его сторонам AB =c, AC = b, BC = a.
треугольника
по его сторонам AB =c, AC = b, BC = a.
Решение. Воспользуемся
тем, что биссектриса делит сторону треугольника на части, пропорциональные
прилежащим сторонам. Обозначим AC1 = c’, BC1 = c”. Тогда c’ + c” = c и ac’ = bc”. Из этих двух уравнений находим c’ и c”.
![]() ,
, ![]() .
.
Подставляя теперь эти выражения в равенство теоремы
Стюарта, получим (![]() )2c = a2
)2c = a2![]() + b2
+ b2![]() - c
- c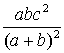 . Откуда
. Откуда
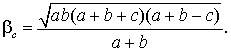
Задача 6. Вычислите медианы треугольника
ABC по его сторонам AB =c, AC
= b, BC = a.
Литература
1. Адамар Ж. Элементарная геометрия. Часть I. Учпедгиз, Москва, 1948.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть I. ОГИЗ, Гостехиздат.
Москва, Ленинград, 1948
3. Зетель С.И. Новая геометрия треугольника. – М.: Учпедгиз, 1962.
4. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1966.
5. Коксетер Г.С.М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука,
1978.
6. Прасолов В.В. Задачи по планиметрии. – Части I, II. – М.: Наука, 1986.